INTRODUCTION
This chapter starts from an exact gate-level reliability analysis of von Neumann multiplexing using majority gates of increasing fan-ins (A = 3, 5, 7, 9, 11) at the smallest redundancy factors (Rp = 2A), and details an accurate device-level analysis. The analysis complements well-known theoretical and simulation results. The gate-level analysis is exact as obtained using exhaustive counting. The extension (of the exact gate-level analysis) to device-level errors will allow us to analyze von Neumann majority multiplexing with respect to device malfunctions. These results explain abnormal behaviors of von Neumann multiplexing reported based on Monte Carlo simulations. These analyses show that device-level reliability results are quite different from the gate-level ones, and could have profound implications for future (nano)circuit designs.
SIA (2005) predicts that the semiconductor industry will continue its success in scaling CMOS for a few more generations. This scaling should become very difficult when approaching 16 nm. Scaling might continue further, but alternative nanodevices might be integrated with CMOS on the same platform. Besides the higher sensitivities of future ultra-small devices, the simultaneous increase of their numbers will create the ripe conditions for an inflection point in the way we deal with reliability.
With geometries shrinking the available reliability margins of the future nano(devices) are considerably being reduced (Constantinescu, 2003), (Beiu et al., 2004). From the chip designers' perspective, reliability currently manifests itself as time-dependent uncertainties and variations of electrical parameters. In the nano-era, these device-level parametric uncertainties are becoming too high to handle with prevailing worst-case design techniques—without incurring significant penalty in terms of area, delay, and power/energy. The global picture is that reliability looks like one of the greatest threats to the design of future ICs. For emerging nanodevices and their associated interconnects the anticipated probabilities of failures, could make future nano-ICs prohibitively unreliable. The present design approach based on the conventional zero-defect foundation is seriously being challenged. Therefore, fault- and defect-tolerance techniques will have to be considered from the early design phases.
Reliability for beyond CMOS technologies (Hutchby et al., 2002) (Waser, 2005) is expected to get even worse, as device failure rates are predicted to be as high as 10% for single electron technology, or SET (Likharev, 1999), going up to 30% for self-assembled DNA (Feldkamp & Niemeyer, 2006) (Lin et al., 2006). Additionally, a comprehensive analysis of carbon nano tubes for future interconnects (Massoud & Nieuwoudt, 2006) estimated the variations in delay at about 60% from the nominal value. Recently, defect rates of 60% were reported for a 160 Kbit molecular electronic memory (Green et al., 2007). Achieving 100% correctness with 1012 nanodevices will be not only outrageously expensive, but plainly impossible! Relaxing the requirement of 100% correctness should reduce manufacturing, verification, and testcosts, while leading to more transient and permanent errors. It follows that most (if not all) of these errors will have to be compensated by architectural techniques (Nikolic et al., 2001) (Constantinescu, 2003) (Beiu et al., 2004) (Beiu & Ruckert, 2009).
From the system design perspective errors fall into: permanent (defects), intermittent, and transient (faults). The origins of these errors can be found in the manufacturing process, the physical changes appearing during operation, as well as sensitivity to internal and external noises and variations. It is not clear if emerging nanotechnologies will not require new fault models, or if multiple errors might have to be dealt with. Kuo (2006) even mentioned that: "we are unsure as to whether much ofthe knowledge that is based on past technologies is still validfor reliability analysis." The well-known approach for fighting against errors is to incorporate redundancy: either static (in space, time, or information) or dynamic (requiring fault detection, location, containment, and recovery). Space (hardware) redundancy relies on voters (generic, inexact, mid-value, median, weighted average, analog, hybrid, etc.) and includes: modular redundancy, cascaded modular redundancy, and multiplexing like von Neumann multiplexing vN-MUX (von Neumann, 1952), enhanced vN-MUX (Roy & Beiu, 2004), and parallel restitution (Sadek et al., 2004). Time redundancy is trading space for time, while information redundancy is based on error detection and error correction codes.
This chapter explores the performance of vN-MUX when using majority gates of fan-in A (MAJ-A). The aim is to get a clear understanding of the trade-offs between the reliability enhancements obtained when using MAJ-A vN-MUX at the smallest redundancy factors Rf = 2A (see Fig. 1) on one side, versus both the fan-ins and the unreliable nanodevices on the other side. We shall start by reviewing some theoretical and simulation results for vN-MUX in Background section.
Exact gate-level simulations (as based on an exhaustive counting algorithm) and accurate device-level estimates, including details of the effects played by nanodevices on MAJ-A vN-MUX, are introduced in the Main Focus of the Chapter section. Finally, implications and future trends are discussed in Future Trends, and conclusions and further directions of research are ending this chapter.
BACKGROUND
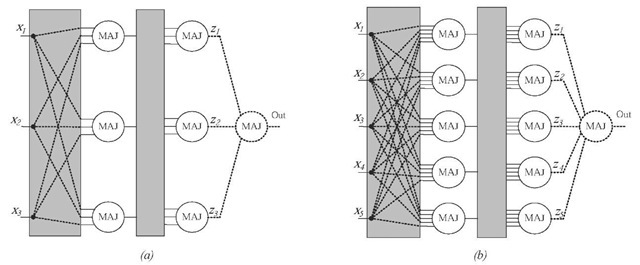
Multiplexing was introduced by von Neumann as a scheme for reliable computations (von Neumann, 1952). vN-MUX is based on successive computing stages alternating with random interconnection stages. Each computing stage contains a set of redundant gates. Although vN-MUX was originally exemplified for NAND-2 it can be implemented using any type of gate, and could be applied to any level of abstraction (subcircuits, gates, or devices). The 'multiplexing' of each computation tries to reduce the likelihood of errors propagating further, by selecting the more-likely result(s) at each stage. Redundancy is quantified by a redundancy factor Rp which indicates the multiplicative increase in the number of gates (subcircuits, or devices). In his original study, von Neumann (1952) assumed independent (un-correlated) gate failures pfGATE and very large RF. The performance ofNAND-2 vN-MUX was compared with other fault-tolerant techniques in (Forshaw et al., 2001), and it was analyzed at lower Rp (30 to 3,000) in (Han & Jonker, 2002), while the first exact analysis at very low RF (3 to 100) for MAJ-3 vN-MUX was done in (Roy & B eiu, 2004).
Figure 1. Minimum redundancy MAJ-A vN-MUX: (a) MAJ-3 (RF = 6); and (b) MAJ-5 (RF = 10)
The issue of which gate should one use is debatable (Ibrahim & Beiu, 2007). It was proven that using MAJ-3 could lead to improved vN-MUX computations only for pfMAJ 3 < 0.0197 (von Neumann, 1952), (Roy & Beiu, 2004). This outperforms the NAND-2 error threshold pfNAND-2 < 0.0107 (von Neumann, 1952), (Sadek et al., 2004). Several other studies have shown that the error thresholds of MAJ are higher than those ofNAND when used in vN-MUX. Evans (1994) proved that:
while the error threshold for NAND-A was determined in (Gao et al., 2005) by solving:
An approach for getting a better understanding of vN-MUX at very small RF is to use Monte Carlo simulations (Beiu, 2005), (Beiu & Sulieman, 2006), (Beiu et al., 2006). These have revealed that the reliability of NAND-2 vN-MUX is in fact better than that of MAJ-3 vN-MUX (at Rf = 6) for small geometrical variations v. As opposed to the theoretical results—where the reliability of MAJ-3 vN-MUX is always better than NAND-2 vN-MUX—the Monte Carlo simulations showed that MAJ-3 vN-MUX is better than NAND-2 vN-MUX, but only for v > 3.4%. Such results were neither predicted (by theory) nor suggested by (gate-level) simulations.
It is to be highlighted here that all the theoretical publications discuss unreliable organs, gates, nodes, circuits, or formulas, but very few mention devices. For getting a clear picture we have started by developing an exhaustive counting algorithm which exactly calculates the reliability of MAJ-A vN-MUX (Beiu et al., 2007). The probability of failure of MAJ-A vN-MUX is:
The results based on exhaustive counting when varying pfMAJ A have confirmed both the theoretical and the simulation ones. MAJ-A vN-MUX at the minimum redundancy factor Rp = 2A improves the reliability over MAJ-A when pfMAJA < 10%, and increasing A increases the reliability. When pfMAJ A 10%, using vN-MUX increases the reliability over that of MAJ-A as long as pfMAJ A is lower than a certain error threshold. If pfMAJ A is above the error threshold, the use of vN-MUX is detrimental, as the reliability of the system is lower than that ofMAJ-A. Still, these do not explain the Monte Carlo simulation results mentioned earlier.
MAIN FOCUS OF THE CHAPTER
Both the original vN-MUX study and the subsequent theoretical ones have considered unreliable gates. They did not consider the elementary devices, and assumed that the gates have a fixed (bounding) pfQKTE. This assumption ignores the fact that different gates are built using different (numbers of) devices, logic styles, or (novel) technological principles. While a standard CMOS inverter has 2 transistors, NAND-2 and MAJ-3 have 4 and respectively 10 transistors. Forshaw et al. (2001) suggested that pfGATE could be estimated as:
where s denotes the probability of failure of a nanode-vice (e.g., transistor, junction, capacitor, molecule, quantum dot, etc.), and n is the number of nanodevices a gate has.
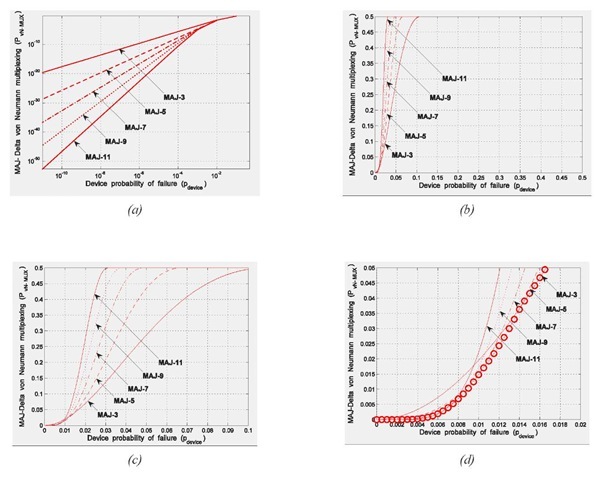
Using eq. 4 as pfMAJ A = 1 - (1 - s)2A the reliabilities have been estimated by modifying the exact counting results reported in (Beiu et al., 2007). The device-level estimates can be seen in Fig. 2. They show that increasing A will not necessarily increase the reliability of MAJ-A vN-MUX (over MAJ-A). This is happening because MAJ-A with larger A require more nanodevices. In particular, while MAJ-11 vN-MUX is the best solution for s < 1%o (Fig. 2(a)), it becomes the worst for s > 2% (Fig. 2(b)). Hence, larger fan-ins are advantageous for lower s (< 1%o), while small fan-ins perform better for larger s (> 1%). Obviously, there is a "swapping" region where the ranking is being reversed. We detail Fig. 2(b) for s > 1% (Fig. 2(c)) and for the "swapping" region 1%o < s < 2% (Fig. 2(d), where 'o' marks show the envelope). These results imply that increasing A and/or Rf does not necessarily improve the overall system's reliability. This is because increasing A and/or RF leads to increasing the number of nanodevices:
Fig. 2. Probability of failure of MAJ-A vN-MUX plotted versus the probability of failure of the elementary (nano)device e: (a) small e (< 1%o); (b) large e (> 1%); (c) detail for e in between 1% and 10%; (d) detailed view of the "swapping" region (e in between 1% and 2%)
This quadratic dependence on A has to be accounted for. Basically, it is s and the number of devices N, and not (only) RF and pfGATE, which should be used when trying to accurately predict the advantages of vN-MUX—or of any other redundancy scheme.
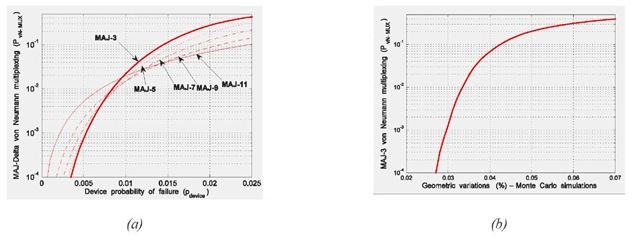
The next step we took was to compare the device-level estimates of MAJ-A vN-MUX (Fig. 3(a)), with the Monte Carlo simulation ones (Fig. 3(b), adapted from (Beiu, 2005) (Beiu & Sulieman, 2006)). The two plots in Fig. 3 have the same vertical scale and exhibit similar shapes. Still, a direct comparison is not trivial as these are mapped against different variables (s and respectively v). This similarity makes us confident that the estimated results are accurate and supporting the claim that a simple estimate for pfGATE leads to good approximations at the system level. For other insights the interested reader should consult (Anghel & Nico-laidis, 2007) and (Martorell et al., 2007).
Figure 3. Probability of failure of MAJ-3 vN-MUX: (a) using device-level estimates and exact counting results; (b) C-SET Monte Carlo simulations for MAJ-3 vN-MUX
FUTURE TRENDS
In a first set of experiments, we compared the reliability of MAJ-A with the reliability of MAJ-A vN-MUX at Rf = 2A. For device-level analyses this is not obvious anymore as MAJ-A are not on a 45° line, which makes it hard to understand where and by how much vN-MUX improves over MAJ-A. The results ofthese simulations can be seen in Fig. 4, where we have used the same interval s e [0, 0.11] on the horizontal axis. Here again it looks like the smallest fan-in is the best.
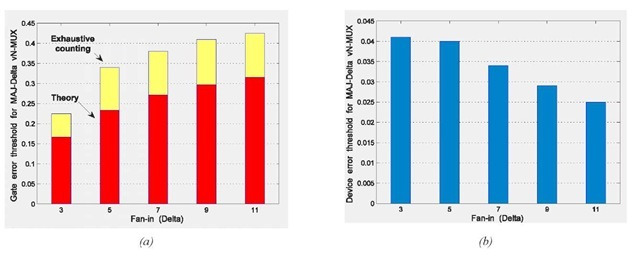
A second set of experiments has studied the effect of changing A on the error threshold of MAJ-A vN-MUX. Fig. 5(a) shows the theoretical gate-level error thresholds (using eq. (1)), as well as the achievable gate-level error thresholds evaluated based on simulations using the exhaustive counting algorithm. Fig. 5(a) shows that the exact gate-level error thresholds are higher than the theoretical gate-level error threshold values (by about 33%). It would appear that one could always enhance reliability by going for a larger fan-in. The extension to device-level estimates can be seen in Fig. 5(b), which reveals a completely different picture. These results imply that:
• device-level error thresholds are about 10x less than the gate-level error thresholds;
• device-level error thresholds are decreasing with increasing to fan-ins (exactly the opposite of gate-level error thresholds);
• for vN-MUX, the highest device-level error threshold of about 4% is achieved when using MAJ-3.
CONCLUSION
This chapter has presented a detailed analysis of MAJ-A vN-MUX for very small fan-ins: exact for the gate-level and estimated but accurate for the device-level. The main conclusions are as follows.
• Exact gate-level error thresholds for MAJ-A vN-MUX are about 33% better than the theoretical ones and increase with increasing fan-in.
• Estimated device-level error thresholds are about 10x lower than gate-level error thresholds and are decreasing with increasing fan-ins—making smaller fan-ins better (Beiu & Makaruk, 1998), (Ibrahim & Beiu, 2007).
• The abnormal (nonlinear) behavior of vN-MUX (Beiu, 2005), (Beiu & Sulieman, 2006) is due to the fact that the elementary gates are made of unreliable nanodevices (implicitly accounted for by Monte Carlo simulations, but neglected by theoretical approaches and gate-level simulations).
Figure 4. Probability of failure ofMAJ-A and MAJ-A vN-MUX plotted versus the device probability offailure e: (a) A = 3; (b) A = 5; (c) A = 7; (d) A = 9. For uniformity, the same interval e e [0, 0.11] was used for all the plots
• Extending the exact gate-level simulations to device-level estimates using 1 - (1 - s)n, leads to quite accurate approximations (as compared to Monte Carlo simulations).
• Device-level estimates show much more complex behaviors than those revealed by gate-level analyses (nonlinear for large s, leading to multiple and intricate crossings).
• Device-level estimates suggest that reliability optimizations for large s will be more difficult than what was expected from gate-level analyses.
• One way to maximize reliability when s is large and unknown (e.g., time varying (Srinivasan et al., 2005)) is to rely on 'adaptive' gates, so neural-inspiration should play a(n important) role in future nano-IC designs (Beiu & Ibrahim, 2007).
Figure 5. Error thresholds for MAJ-A vN-MUX versus fan-in A: (a) gate-level error threshold, both theoretical (red) and exact (yellow) as obtained through exhaustive counting; (b) device-level error threshold
Finally, precision is very important as "small errors ... have a huge impact in estimating the required level of redundancy for achieving a specified/target reliability" (Roelke et al., 2007). It seems that the current gate-level models tend to underestimate reliability, while we do not do a good job at the device-level, with Monte Carlo simulation the only widely used method. More precise estimates than the ones presented in this chapter are possible using Monte Carlo simulations in combination with gate-level reliability algorithms. These are clearly needed and have just started to be investigated (Lazarova-Molnar et al., 2007).
KEY TERMS
Circuit: Network of devices.
Counting (Exhaustive): The mathematical action of repeated addition (exhaustive considers all possible combinations).
Device: Any physical entity deliberately affecting the information carrying particle (or their associated fields) in a desired manner, consistent with the intended function of the circuit.
Error Threshold: The probability of failure of a component (gate, device) above which the multiplexed scheme is not able to improve over the component itself.
Fan-In: Number of inputs (to a gate).
Fault-Tolerant: The ability of a system (circuit) to continue to operate rather than failing completely (possibly at a reduced performance level) in the event of the failure of some of its components.
Gate (Logic): Functional building block (in digital logic a gate performs a logical operation on its logic inputs).
Majority (Gate): A logic gate of odd fan-in which outputs a logic value equal to that of the majority of its inputs.
Monte Carlo: A class of stochastic (by using pseudorandom numbers) computational algorithms for simulating the behaviour of physical and mathematical systems.
Multiplexing (von Neumann): A scheme for reliable computations based on successive computing stages alternating with random interconnection stages (introduced by von Neumann in 1952).
Redundancy (Factor): Multiplicative increase in the number of (identical) components (subsystems, blocks, gates, devices), which can (automatically) replace (or augment) failing component(s).
Reliability: The ability of a circuit (system, gate, device) to perform and maintain its function(s) under given (as well as hostile or unexpected) conditions, for a certain period of time.

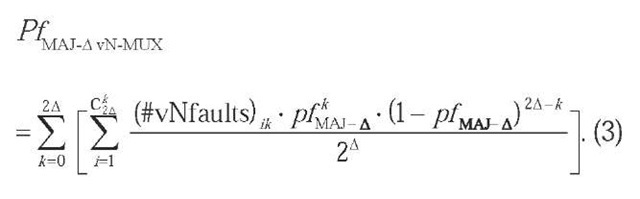
![Probability offailure ofMAJ-A and MAJ-A vN-MUX plotted versus the device probability offailure e: (a) A = 3; (b) A = 5; (c) A = 7; (d) A = 9. For uniformity, the same interval e e [0, 0.11] was used for all the plots Probability offailure ofMAJ-A and MAJ-A vN-MUX plotted versus the device probability offailure e: (a) A = 3; (b) A = 5; (c) A = 7; (d) A = 9. For uniformity, the same interval e e [0, 0.11] was used for all the plots](http://lh4.ggpht.com/_1wtadqGaaPs/TH_i9iPO7tI/AAAAAAAAXUE/4DBKXQDUMVs/tmp7E87_thumb_thumb2.jpg?imgmax=800)