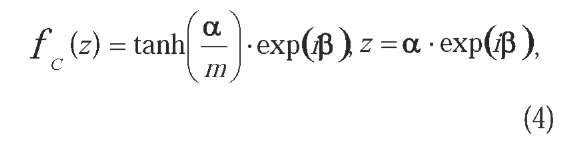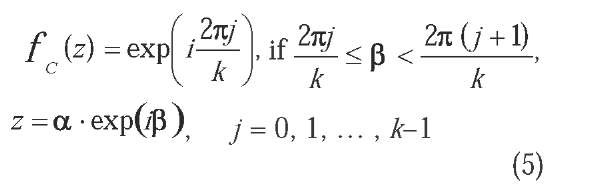INTRODUCTION
The usual real-valued artificial neural networks have been applied to various fields such as telecommunications, robotics, bioinformatics, image processing and speech recognition, in which complex numbers (two dimensions) are often used with the Fourier transformation. This indicates the usefulness of complex-valued neural networks whose input and output signals and parameters such as weights and thresholds are all complex numbers, which are an extension of the usual real-valued neural networks. In addition, in the human brain, an action potential may have different pulse patterns, and the distance between pulses may be different. This suggests that it is appropriate to introduce complex numbers representing phase and amplitude into neural networks.
Aizenberg, Ivaskiv, Pospelov and Hudiakov (1971) (former Soviet Union) proposed a complex-valued neuron model for the first time, and although it was only available in Russian literature, their work can now be read in English (Aizenberg, Aizenberg & Vandewalle, 2000). Prior to that time, most researchers other than Russians had assumed that the first persons to propose a complex-valued neuron were Widrow, McCool and Ball (1975). Interest in the field of neural networks started to grow around 1990, and various types of complex-valued neural network models were subsequently proposed. Since then, their characteristics have been researched, making it possible to solve some problems which could not be solved with the real-valued neuron, and to solve many complicated problems more simply and efficiently.
BACKGROUND
The generic definition of a complex-valued neuron is as follows. The input signals, weights, thresholds and output signals are all complex numbers. The net input U to a complex-valued neuron n is defined as:
where Wm is the complex-valued weight connecting complex-valued neurons n and m, Xm is the complex-valued input signal from the complex-valued neuron m, and V is the complex-valued threshold of the neuron n. The output value of the neuron nis given by fC (U^ where fC : C— C is called activation function (C denotes the set of complex numbers). Various types of activation functions used in the complex-valued neuron have been proposed, which influence the properties of the complex-valued neuron, and a complex-valued neural network consists of such complex-valued neurons.
For example, the component-wise activation function or real-imaginary type activation function is often used (Nitta & Furuya, 1991; Benvenuto & Piazza, 1992; Nitta, 1997), which is defined as follows:
where f,(u) = 1/(1+exp(-u)), ue R (Rdenotes the set of real numbers), idenotes V-1, and the net input Un is converted into its real and imaginary parts as follows:
That is, the real and imaginary parts of an output of a neuron mean the sigmoid functions of the real part x and imaginary part y of the net input z to the neuron, respectively.
Note that the component-wise activation function (eqn (2)) is bounded but non-regular as a complex-valued function because the Cauchy-Riemann equations do not hold. Here, as several researchers have pointed out (Georgiou & Koutsougeras, 1992; Nitta, 1997) in the complex region, we should recall the Liouville's theorem, which states that if a function g is regular at all z 6 C and bounded, then g is a constant function. That is, we need to choose either regularity or boundedness for an activation function of complex-valued neurons. In addition, it has been proved that the complex-valued neural network with the component-wise activation function (eqn (2)) can approximate any continuous complex-valued function, whereas a network with a regular activation function (for example, fC(z) = 1/(1+exp(-z)) (Kim & Guest, 1990), and fC(z) = tanh (z) (Kim & Adali, 2003)) cannot approximate any non-regular complex-valued function (Arena, Fortuna, Re & Xibilia, 1993; Arena, Fortuna, Muscato & Xibilia, 1998). That is, the complex-valued neural network with the non-regular activation function (eqn (2)) is a universal approximator, but a network with a regular activation function is not. It should be noted here that the complex-valued neural network with a regular complex-valued activation function such as fc(z) = tanh (z) with the poles can be a universal approximator on the compact subsets of the deleted neighbourhood of the poles (Kim & Adali, 2003). This fact is very important theoretically, however, unfortunately the complex-valued neural network for the analysis is not usual, that is, the output of the hidden neuron is defined as the product of several activation functions. Thus, the statement seems to be insufficient to compare with the case of component-wise complex-valued activation function. Thus, the ability of complex-valued neural networks to approximate complex-valued functions depends heavily on the regularity of activation functions used.
On the other hand, several complex-valued activation functions based on polar coordinates have been proposed. For example, Hirose (1992) proposed the following amplitude-phase type activation function:
where m is a constant. Although this amplitude-phase activation function is not regular, Hirose noted that the non-regularity did not cause serious problems in real applications and that the amplitude-phase framework is suitable for applications in many engineering fields such as optical information processing systems, and amplitude modulation, phase modulation and frequency modulation in electromagnetic wave communications and radar. Aizenberg et al. (2000) proposed the following activation function:
where k is a constant. Eqn (5) can be regarded as a type of amplitude-phase activation functions. Only phase information is used and the amplitude information is discarded, however, many successful applications show that the activation function is sufficient.
INHERENT PROPERTIES OF THE MULTI-LAYERED TYPE COMPLEX-VALUED NEURAL NETWORK
This article presents the essential differences between multi-layered type real-valued neural networks and multi-layered type complex-valued neural networks, which are very important because they expand the real application fields of the multi-layered type complex-valued neural networks. To the author's knowledge, the inherent properties of complex-valued neural networks with regular complex-valued activation functions have not been revealed except their learning performance so far. Thus, only the inherent properties of the complex-valued neural network with the non-regular complex-valued activation function (eqn (2)) are mainly described: (a) the learning performance, (b) the ability to transform geometric figures, and (c) the orthogonal decision boundary.
Learning Performance
In the applications of multi-layered type real-valued neural networks, the error back-propagation learning algorithm (called here, Real-BP) (Rumelhart, Hinton & Williams, 1986) has often been used. Naturally, the complex-valued version of the Real-BP (called here, Complex-BP) can be considered, and was actually proposed by several researchers (Kim & Guest, 1990; Nitta & Furuya, 1991; Benvenuto & Piazza, 1992; Georgiou & Koutsougeras, 1992; Nitta, 1993, 1997; Kim &Adali, 2003). This algorithm enables the network to learn complex-valued patterns naturally.
It is known that the learning speed of the Complex-BP algorithm is faster than that of the Real-BP algorithm. Nitta (1991, 1997) showed in some experiments on learning complex-valued patterns that the learning speed is several times faster than that of the conventional technique, while the space complexity (i.e., the number of learnable parameters needed) is only about half that of Real-BP. Furthermore, De Azevedo, Travessa and Argoud (2005) applied the Complex-BP algorithm of the literature (Nitta, 1997) to the recognition and classification of epileptiform patterns in EEG, in particular, dealing with spike and eye-blink patterns, and reconfirmed the superiority of the learning speed of the Complex-BP described above. As for the regular complex-valued activation function, Kim and Adali (2003) compared the learning speed of the Complex-BP using nine regular complex-valued activation functions with those of the Complex-BP using three non-regular complex-valued activation functions (including eqn (4)) through a computer simulation for a simple nonlinear system identification example. The experimental results suggested that the Complex-BP with the regular activation function f (z) = arcsin h(z) was the fastest among them.
Ability to Transform Geometric Figures
The Complex-BP with the non-regular complex-valued activation function (eqn (2)) can transform geometric figures, e.g. rotation, similarity transformation and parallel displacement of straight lines, circles, etc., whereas the Real-BP cannot (Nitta, 1991, 1993, 1997). Numerical experiments suggested that the behaviour of a Complex-BP network which learned the transformation of geometric figures was related to the Identity Theorem in complex analysis.
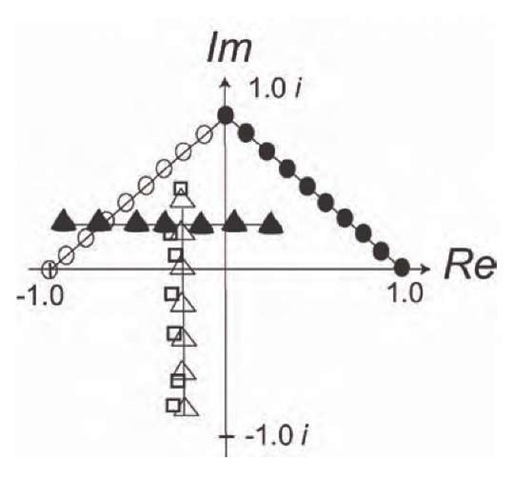
Only an illustrative example on a rotation is given below. In the computer simulation, a 1-6-1 three-layered complex-valued neural network was used, which transformed a point (x, y) into (x', y') in the complex plane. Although the Complex-BP network generates a value z within the range 0 < Re[z], Im[z] < 1 due to the activation function used (eqn (2)), for the sake of convenience it is presented in the figure given below as having a transformed value within the range - 1 < Re[z], Im[z] < 1. The learning rate used in the experiment was 0.5. The initial real and imaginary components of the weights and the thresholds were chosen to be random real numbers between 0 and 1. The experiment consisted of two parts: a training step, followed by a test step. The training step consisted of learning a set of (complex-valued) weights and thresholds, such that the input set of (straight line) points (indicated by black circles in Fig. 1) gave as output, the (straight line) points (indicated by white circles) rotated counterclockwise over p/2 radians. Input and output pairs were presented 1,000 times in the training step. These complex-valued weights and thresholds were then used in a test step, in which the input points lying on a straight line (indicated by black triangles in Fig. 1) would hopefully be mapped to an output set of points lying on the straight line (indicated by white triangles) rotated counterclockwise over p/2 radians. The actual output test points for the Complex-BP did, indeed, lie on the straight line (indicated by white squares). It appears that the complex-valued network has learned to generalize the transformation of each point Zk (= rk exp[i0 k ]) into Zk exp[ia ](= rk exp[i(0 k+a)]), i.e., the angle of each complex-valued point is updated by a complex-valued factor exp[ia], however, the absolute length of each input point is preserved. In the above experiment, the 11 training input points lay on the line y = - x + 1 (0 < x < 1) and the 11 training output points lay on the line y = x + 1 (- 1 < x < 0). The seven test input points lay on the line y=0.2 (- 0.9 < x < 0.3). The desired output test points should lie on the line x = - 0.2.
Watanabe, Yazawa, Miyauchi and Miyauchi (1994) applied the Complex-BP in the field of computer vision. They successfully used the ability to transform geometric figures of the Complex-BP network to complement the 2D velocity vector field on an image, which was derived from a set of images and called an optical flow. The ability to transform the geometric figure of the Complex-BP can also be used to generate fractal images. Actually, Miura and Aiyoshi (2003) applied the Complex-BP to the generation of fractal images and showed in computer simulations that some fractal images such as snow crystals could be obtained with high accuracy where the iterated function systems (IFS) were constructed using the ability to transform geometric figure of the Complex-BP.
Orthogonal Decision Boundary
The decision boundary of the complex-valued neuron with the non-regular complex-valued activation function (eqn (2)) has a different structure from that of the real-valued neuron. Consider a complex-valued neuron with M input neurons. Let the weights denote
w = l[w wM = wr+ i W, wr= t[w1r wMr], w = t[w1i w,/] and let the threshold denote d = d r+ i di. Then,
... M' ' for Minput signals (complex numbers) z = l[z zM] = x + iy, x = t[x1... xM], y = t[y1 ... yM], the complex-valued neuron generates
Note here that eqn (7) is the decision boundary for the real part of an output of the complex-valued neuron with M inputs. That is, input signals (x, y) 6 R2M are classified into two decision regions {(x, y) 6 R2M | X(x, y) > CR} and {(x, y) 6 R2M | X(x, y) < CR} by the hypersurface given by eqn (7). Similarly, eqn (8) is the decision boundary for the imaginary part. Noting that the inner product of the normal vectors of the decision boundaries (eqns (7) and (8)) is zero, we find that the decision boundary for the real part of an output of a complex-valued neuron and that for the imaginary part intersect orthogonally.
As is well known, the XOR problem and the detection of symmetry problem cannot be solved with a single real-valued neuron (Rumelhart, Hinton & Williams, 1986). Contrary to expectation, it was proved that such problems could be solved by a single complex-valued neuron with the orthogonal decision boundary, which revealed the potent computational power of complex-valued neural networks (Nitta, 2004a).
FUTURE TRENDS
Many application results (Hirose, 2003) such as associative memories, adaptive filters, multi-user communication and radar image processing suggest directions for future research on complex-valued neural networks.
It is natural that the inherent properties of the multi-layered type complex-valued neural network with non-regular complex-valued activation function (eqn (2)) are not limited to the ones described above. Furthermore, to the author's knowledge, the inherent properties except the learning performance of recurrent type complex-valued neural networks have not been reported. The same is also true of the complex-valued neural network with regular complex-valued activation functions. Such exploration will expand the application fields of complex-valued neural networks.
In the meantime, efforts have already been made to increase the dimensionality of neural networks, for example, three dimensions (Nitta, 2006), quaternions (Arena, Fortuna, Muscato & Xibilia, 1998; Isokawa, Kusakabe, Matsui & Peper, 2003; Nitta, 2004b), Clifford algebras (Pearson & Bisset, 1992; Buchholz & Sommer, 2001), and ^dimensions (Nitta, 2007), which is a new direction for enhancing the ability of neural networks.
CONCLUSION
This article outlined the inherent properties of complex-valued neural networks, especially those of the case with non-regular complex-valued activation functions, that is, (a) the learning performance, (b) the ability to transform geometric figures, and (c) the orthogonal decision boundary. Successful applications of such networks were also described.
KEY TERMS
Artificial Neural Network: A network composed of artificial neurons. Artificial neural networks can be trained to find nonlinear relationships in data.
Back-Propagation Algorithm: A supervised learning technique used for training neural networks, based on minimizing the error between the actual outputs and the desired outputs.
Clifford Algebras: An associative algebra, which can be thought of as one of the possible generalizations of complex numbers and quaternions.
Complex Number: A number of the form a + ib where a and b are real numbers, and i is the imaginary unit such that i2 = - 1. a is called the real part, and b the imaginary part.
Decision Boundary: A boundary which pattern classifiers such as the real-valued neural network use to classify input patterns into several classes. It generally consists of hypersurfaces.
Identity Theorem: A theorem for regular complex functions: given two regular functions f and g on a connected open set D, if f = g on some neighborhood of z that is in D, then f = g on D.
Quaternion: A four-dimensional number which is a non-commutative extension of complex numbers.
Regular Complex Function: A complex function that is complex-differentiable at every point.
Figure 1. Rotation of a straight line. A black circle denotes an input training point, a white circle an output train -ing point, a black triangle an input test point, a white triangle a desired output test point, and a white square an output test point generated by the Complex-BP network.