INTRODUCTION
Applying biological concepts to create new models in the computational field is not a revolutionary idea: science has already been the basis for the famous artificial neuron models, the genetic algorithms, etc. The cells of a biological organism are able to compose very complex structures from a unique cell, the zygote, with no need for centralized control (Watson J.D. & Crick F. H. 1953). The cells can perform such process thanks to the existence of a general plan, encoded in the DNA for the development and functioning of the system. Another interesting characteristic of natural cells is that they form systems that are tolerant to partial failures: small errors do not induce a global collapse of the system. Finally, the tissues that are composed by biological cells present parallel information processing for the coordination of tissue functioning in each and every cell that composes this tissue.
All the above characteristics are very interesting from a computational viewpoint. This paper presents the development of a model that tries to emulate the biological cells and to take advantage of some of their characteristics by trying to adapt them to artificial cells. The model is based on a set of techniques known as Artificial Embryology (Stanley K. & Miikkulainen R. 2003) or Embryology Computation (Kumar S. & Bentley P.J 2003).
BACKGROUND
The Evoluationary Computation (EC) field has given rise to a set of models that are grouped under the name ofArtificial Embryology (AE), first introduced by Stanley and Miikkulainnen (Stanley K. & Miikkulainen R. 2003). This group refers to all the models that try to apply certain characteristics of biological embryonic cells to computer problem solving, i.c. self-organisation, failure tolerance, and parallel information processing.
The work on AE has two points of view. On the one hand can be found the grammatical models based on L-systems (LindenmayerA. 1968) which do a top-down approach to the problem. On the other hand can be found the chemical models based on the Turing's ideas (Turing A. 1952) which do a down-top approach.
On the last one, the starting point of this field can be found in the modelling of gene regulatory networks, performed by Kauffmann in 1969 (Kauffman S.A. 1969). After that, several works were carried out on subjects such as the complex behaviour generated by the fact that the differential expression of certain genes has a cascade influence on the expressions of others (Mjolsness E., Sharp D.H., & Reinitz J. 1995).
The work performed by the scientific community can be divided into two main branches. The more theoretical branch uses the emulation of cell capabilities such as cellular differentiation and metabolism (Kitano H. 1994; Kaneko K. 2006) to create a model that functions as a natural cell. The purpose of this work is to do an in-depth study of the biological model.
The more practical branch mainly focuses on the development of a cell inspired-model that might be applicable to other problems (Bentley, P.J., Kumar, S. 1999; Kumar, S. 2004). According to this model, every cell would not only have genetic information that encodes the general performance of the system, it would also act as a processor that communicates with the other cells. This model is mainly applied to the solution of simple 3D spatial problems, robot control, generative encoding for the construction of artificial organisms in simulated physical environments and real robots, or to the development of the evolutionary design of hardware and circuits (Endo K., Maeno T. & Kitano H 2003; Tufte G. & Haddow P. C. 2005).
Considering the gene regulatory networks works, the most relevant models are the following: the Kumar and Bentley model (Kumar S. & Bentley P.J 2003), which uses the Bentley's theory of fractal proteins (Bentley, P.J. 1999); for the calculation of protein concentration; the Eggenberger model (Eggenberger P. 1996), which uses the concepts of cellular differentiation and cellular movement to determine cell connections; and the work of Dellaert and Beer (Dellaert F. & Beer R.D. 1996), who propose a model that incorporates the idea of biological operons to control the model expression, where the function assumes the mathematical meaning of a Boolean function.
All these models can be regarded as special cellular automata. In cellular automata, a starting cell set in a certain state will turn into a different set of cells in different states when the same transition function (Conway J.H. 1971) is applied to all the cells during a determined lapse of time in order to control the message concurrence among them. The best known example of cellular automats is Conway's "Game of Life", where this behaviour can be observed perfectly. Whereas the classical conception specifies the behaviour rules, the evolutionary models establish the rules by searching for a specific behaviour. This difference comes from the mathematical origin of the cellular automats, whereas the here presented models are based on biology and embryology.
These models should not be confused with other concepts that might seem similar, such as Gene Expression Programming (GEP) (Ferreira C. 2006).Although GEP codifies the solution in a string, similarly as how it is done in the present work, the solution program is developed in a tree shape, as in classical genetic programming (Koza, J. et. al.1999) which has little or nothing in common with the presented models.
ARTIFICIAL EMBRYOGENY MODEL
The cells of a biological system are mainly determined by the DNA strand, the genes, and the proteins contained by the cytoplasm. The DNA is the structure that holds the gene-encoded information that is needed for the development of the system. The genes are activated or transcribed thanks to the protein shaped-information that exists in the cytoplasm, and consist of two main parts: the sequence, which identifies the protein that will be generated if the gene is transcribed, and the promoter, which identifies the proteins that are needed for gene transcription.
Another remarkable aspect of biological genes is the difference between constitutive genes and regulating genes. The latter are transcribed only when the proteins identified in the promoter part are present. The constitutive genes are always transcribed, unless inhibited by the presence of the proteins identified in the promoter part, acting then as gene oppressors.
The present work has tried to partially model this structure with the aim of fitting some of its abilities into a computational model; in this way, the system would have a structure similar that is similar to the above and will be detailed in the next section.
Proposed Model
Various model variants were developed on the basis of biological concepts. The proposed artificial cellular system is based on the interaction of artificial cells by means of messages that are called proteins. These cells can divide themselves, die, or generate proteins that will act as messages for themselves as well as for neighbour cells.
The system is supposed to express a global behaviour towards the generation of structures in 2D. Such behaviour would emerge from the information encoded in a set of variables of the cell that, in analogy with the biological cells, will be named genes.
One promising application, in which we are working, could be the compact encoding of adaptive shapes, similar to the functioning of fractal growth or the fractal image compression.
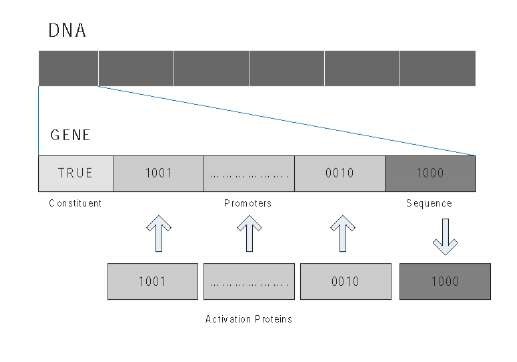
Figure 1. Structure of a system gene
The central element of our model is the artificial cell. Every cell has a binary string-encoded information for the regulation of its functioning. Following the biological analogy, this string will be called DNA. The cell also has a structure for the storage and management of the proteins generated by the own cell and those received from neighbourhood cells; following the biological model, this structure is called cytoplasm.
The DNA of the artificial cell consists of functional units that are called genes. Each gene encodes a protein or message (produced by the gene). The structure of a gene has four parts (see Figure 1):
• Sequence: the binary string that corresponds to the protein that encodes the gene
• Promoters: is the gene area that indicates the proteins that are needed for the gene's transcription.
• Constituent: this bit identifies if the gene is constituent or regulating
• Activation percentage (binary value): the percentage of minimal concentration of promoters proteins inside the cell that causes the transcription of the gene.
The other fundamental element for keeping and managing the proteins that are received or produced by the artificial cell is the cytoplasm. The stored proteins have a certain life time before they are erased. The cytoplasm checks which and how many proteins are needed for the cell to activate the DNA genes, and as such responds to all the cellular requirements for the concentration of a given type of protein. The cytoplasm also extracts the proteins from the structure in case they are needed for a gene transcription.
Model Functioning
The functioning of genes is determined by their type, which can be constituent or regulating. The transcription of the encoded protein occurs when the promoters of the non-constituent genes appear in a certain rate at the cellular cytoplasm. On the other hand, the constituent genes are expressed during all the "cycles" until such expression is inhibited by the present rate of the promoter genes.
The activation of the regulating genes or the inhibition of the constituent genes is achieved if the condition expressed by Eq.1 is fulfilled, where Protein Concentration Percentage represents the cytoplasm concentration of the protein that is being considered; Distance stands for the Hamming distance between one promoter and the considered protein; and Activation Percentage is the minimal percentage needed for the gene activation that is encoded in the gene. This equation is tested on each promoter and each protein. If the condition is fulfilled for all the promoters, that gene is transcribed. According to this, if gene-like promoters exist in a concentration higher than the encoded concentration, they can also induce its transcription, similarly to what happens in biology and therefore providing the model with higher flexibility. Ifthe condition is fulfilled for each promoter, the gene is activated and therefore transcribed.
After the activation of one of the genes, three things can happen: the generated protein may be stored in the cell cytoplasm, it may be communicated to the neighbour cells, or it may induce cellular division (mitosis) and/or death (apoptosis). The different events of a tissue are managed in the cellular model by means of "cellular cycles". Such "cycles" will contain all the actions that can be carried out by the cells, restricting sometimes their occurrence. The "cellular cycles" can be described as follows:
• Actualisation of the life time of proteins in the cytoplasm
• Verification of the life status of the cell (cellular death)
• Calculation of the genes that react and perform the special behaviour that may be associated to them
• Communication between proteins
Solution Search
A classical approach of EC proposes the use of Genetic Algorithms (GA) (Fogel L.J., Owens A. J. & Walsh M.A. 1966; Goldberg D.E. 1989; Holland J.H. 1975) for the optimisation, in this case, of the values of the DNA genes (binary strands). Each individual of the GA population will represent a possible DNA strand for problem solving.
In order to calculate the fitness value for every individual in the GA or the DNA, the strand is introduced into an initial cell or zygote. After simulating during a certain number of cycles, the contained information is expressed and the characteristics of the resulting tissue are evaluated by means of various criteria, according to the goal that is to be achieved.
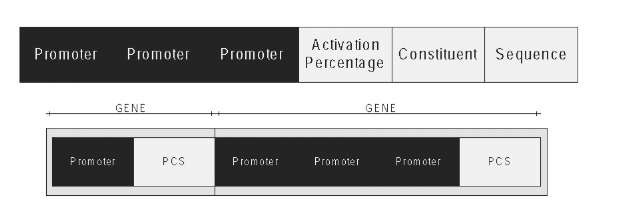
Figure 2. (Above) Three promoters and a PCS structure (Below); Example of GA genes association for the encoding of cellular genes
The encoding of the individual genes follows a structure that is similar to the one described in Figure 2 (Above), where the number of promoters of each gene may, vary but the white and indivisible section "Activation Percentage - Constituent - Sequence" (PCS) must always be present. The PCS sections determine the genes of the individual, and the promoter sections are associated to the PCS sections, as shown in Figure 2(Below).
The search of a set of structures similar to those shown in Figure 2 required the adaptation of the crossover and mutation GA operations to this specific problem. Since the length of the individuals is variable, the crossover had to be performed according to these lengths. When an individual is selected, a random percentage is generated to determine the crossover point of that individual. After selecting the section in that position, a crossover point is chosen for the section selected in the other parent. Once this has been done, the crossover point selection process is repeated in the second selected parent in the same position as in the previous individual. From this stage on, the descendants are composed in the traditional way, since they are two strings of bits. We could execute a normal bit strings crossover, but the previously mentioned steps guarantee that the descendants are valid solutions for the DNA strands transformation.
With regards to mutation, it should be mentioned that the types of the promoter or PCS sections are identified according to the value of the first string bit. Bearing that in mind, together with the variable length of individuals, the mutation operation had to be adapted so that it could modify not only the number of these sections, but also the value of a given section.
The probability of executing the mutation is usually low, but this time it even had to be divided into the three possible mutation operations that the system contemplates. Various tests proved that the most suitable values for the distribution of the different mutation operations, after the selection of a position for mutation, were the following: for 20% ofthe opportunities, a section (either a promoter or a PCS) is added; for another 20%, the existing section is removed; and finally, for the remaining 60% ofthe opportunities, the value of one of the bits of the section is randomly changed. The latter may provoke not only the change of one of the values, but also the change of the section type: if the bit that identifies the section type is changed, the information of that section varies. For instance, if a promoter section turns into a PCS section, the promoter sequence turns into the gene sequence, and constitutive and activation percentage values are generated.
After reaching this development level and presenting the test set in (Fernandez-Blanco E., J., J R., Gestal M. & Pedreira N. 2007), the authors concluded that the bottleneck of the model turned out to be the development of the evaluation functions, since in every new figure the development of the function was time-consuming and not reusable.
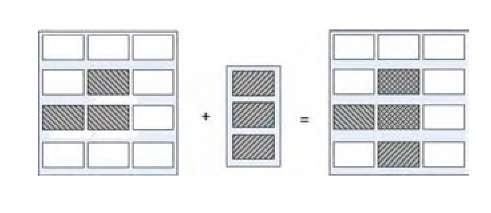
In order to solve this problem, the evaluation function was developed according to the concept of a correction template. From the tissue that is developed by the DNA that is being evaluated, the centroid is calculated. This point would be the center of the solution template, which is merely a matrix of Boolean values representing the figure that is aimed at. The template could be (and usually is) smaller than the development environment of the tissue, which means that every cell that may not be covered by the template will contribute to the tissue error with 1.0. The remaining tissue, covered by the template, will execute the NEXOR Boolean operation in order to obtain the number of differences between the template and the tissue. Each difference contributes with a value of 1.0. to tissue error.
Figure 3. Tissue + Template. Example of Template use.
Figure 3 illustrates the use of this method. We can observe that the error of this tissue with regard to the template is 2, since we generated a cell that is not contemplated by the template, whereas another cell that is present in the template is really missing.
FUTURE TRENDS
The model could also include new characteristics such as the displacement of cells around their environment, or a specialisation operator that blocks pieces of DNA during the expression of its descendants, as happens in the natural model.
Finally, this group is currently working in one of the possible applications of this model: its use for image compression similarly as fractal compression works. The fractal compression searches the parameters of a fractal formula that encodes itself the starting image. The present model searches the gene sequence that might result in the starting image. In this way, the method based on template that has been presented in this paper can be used for performing that search, using the starting image as template.
CONCLUSION
Taking into account the here developed model, we can say that the use of certain properties of biological cellular systems is feasible for the creation of artificial structures that might be used in order to solve certain computational problems.
Some behaviours of the biological model have been also observed in the artificial model: information redundancy in DNA, stability after achieving the desired shape, or variability in gene behaviour.
KEY TERMS
Artificial Cell: Each of the elements that process the orders codified into the DNA.
Artificial Embryogeny: The term overlaps all the processing models which use biological development ideas as inspiration for its functioning.
Cellular Cycle: Cellular development time unit which limits the ocurrents number of certain cellular development actions.
Cytoplasm: Part of an artificial cell which is responsible of management the protein-shaped messages.
DNA: Set of rules which are responsible of the cell behaviour.
Gene: Each of the rules which codifies one action of the cell.
Protein: This term identifies every kind of the messages that receives an artificial cell.
Zygote: The initial cell from where a tissue is generated using the DNA information.