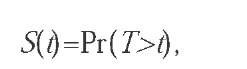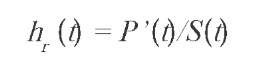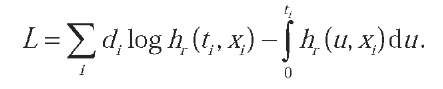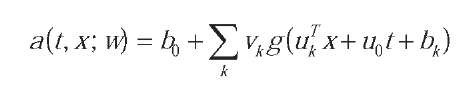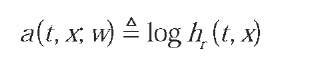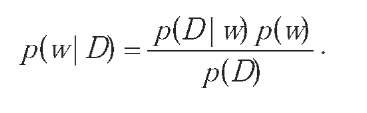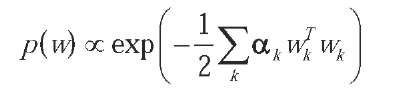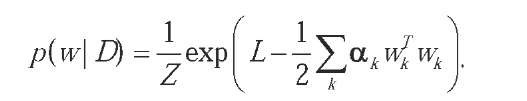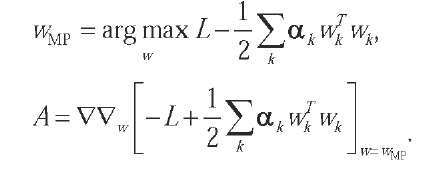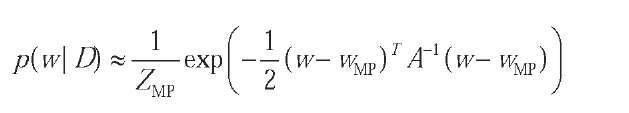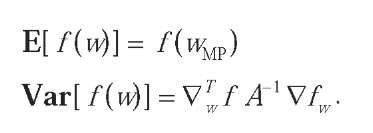INTRODUCTION
Survival analysis is used when we wish to study the occurrence of some event in a population of subjects and the time until the event of interest. This time is called survival time or failure time. Survival analysis is often used in industrial life-testing experiments and in clinical follow-up studies. Examples of application include: time until failure of a light bulb, time until occurrence of an anomaly in an electronic circuit, time until relapse of cancer, time until pregnancy.
In the literature we find many different modeling approaches to survival analysis. Conventional parametric models may involve too strict assumptions on the distributions of failure times and on the form of the influence of the system features on the survival time, assumptions which usually extremely simplify the experimental evidence, particularly in the case of medical data (Cox & Oakes, 1984). In contrast, semi-parametric models do not make assumptions on the distributions of failures, but instead make assumptions on how the system features influence the survival time (the usual assumption is the proportionality of hazards); furthermore, these models do not usually allow for direct estimation of survival times. Finally, non-parametric models usually only allow for a qualitative description of the data on the population level.
Neural networks have recently been used for survival analysis; for a survey on the current use of neural networks, and some previous attempts at neural network survival modeling we refer to (Bakker & Heskes, 1999), (Biganzoli et al., 1998), (Eleuteri et al., 2003), (Lisboa et al., 2003), (Neal, 2001), (Ripley & Ripley, 1998), (Schwarzer et al. 2000).
Neural networks provide efficient parametric estimates of survival functions, and, in principle, the capability to give personalised survival predictions. In a medical context, such information is valuable both to clinicians and patients. It helps clinicians to choose appropriate treatment and plan follow-up efficiently. Patients at high risk could be followed up more frequently than those at lower risk in order to channel valuable resources to those who need them most. For patients, obtaining information about their prognosis is also extremely valuable in terms of planning their lives and providing care for their dependents.
In this article we describe a novel neural network model aimed at solving the survival analysis problem in a continuous time setting; we provide details about the Bayesian approach to modeling, and a sample application on real data is shown.
BACKGROUND
Let Tdenote an absolutely continuous positive random variable, with distribution function P, representing the time of occurrence of an event. The survival function, S(t), is defined as:
that is, the probability of surviving beyond time t. We shall generally assume that the survival function also depends on a set of covariates, represented by the vector x (which can itself be assumed to be a random variable). An important function related to the survival function is the hazard rate (Cox & Oakes, 1984), defined as:
where P' is the density associated to P. The hazard rate can be interpreted as the instantaneous force of mortality.
In many survival analysis applications we do not directly observe realisations of the random variable T; therefore we must deal with a missing data problem. The most common form of missingness is right censoring, i.e., we observe realisations of the random variable:
Z=min(T,C),
where C is a random variable whose distribution is usually unknown. We shall use a censoring indicator d to denote whether we have observed an event (d=1) or not (d=0). It can be shown that inference does not depend on the distribution of C (Cox & Oakes, 1984).
With the above definitions in mind we can now formulate the log-likelihood function necessary for statistical inference. We shall omit the details, and only report the analytical form:
For further details, we refer the reader to (Cox & Oakes, 1984).
CONDITIONAL HAZARD ESTIMATING NEURAL NETWORKS
Neural Network Model
The neural network model we used is the Multi-Layer Perceptron (MLP) (Bishop, 1995):
where g() is a sigmoid function, and w={b0, v, u, u0, b} is the set of network parameters. The MLP output defines an analytical model for the logarithm of the hazard rate function:
We refer to this continuous time model as Conditional Hazard Estimating Neural Network (CHENN).
Bayesian Learning of the Network Parameters
The Bayesian learning framework offers several advantages over maximum likelihood methods commonly used in neural network learning (Bishop, 1995), (MacKay, 1992), among which the most important are automatic regularization and estimation of error bars on predictions.
In the conventional maximum likelihood approach to training, a single weight vector is found, which minimizes the error function; in contrast, the Bayesian scheme considers a probability distribution over weights w. This is described by a prior distributionp(w) which is modified when we observe a dataset D. This process can be expressed by Bayes' theorem:
To evaluate the posterior distribution, we need expressions for the likelihoodp(D\w) (which we have already shown) and for the prior p(w).
The prior over weights should reflect the knowledge, if any, we have about the mapping we want to build. In our case, we expect the function to be very smooth, so an appropriate prior might be:
which is a multivariate normal density with zero mean and diagonal covariance matrix with elements 1/a.. In this way, weights centered on zero have higher probability, a fact which encourages very smooth functions.
Note that the prior is parametric, and the regular-ization parameters ak (which are inverse variances) are called hyperparameters, because they control the distribution of the network parameters.
Note also that the prior is specialized for different groups of weights by using different regularization parameters for each group; this is done to preserve the scaling properties of network mappings (Bishop, 1995), (MacKay, 1992). This prior is called Automatic Relevance Determination (ARD). This scheme defines a model whose prior over the parameters embodies the concept of relevance, so that the model is effectively able to infer which parameters are relevant based on the training data and then switch the others off (or at least reduce their influence on the overall mapping).
The ARD modeling scheme in the case of the CHENN model defines weight groups for the inputs, the output layer weights, and the biases.
Once the expressions for the prior and the noise model are given, we can evaluate the posterior:
This distribution is usually very complex and mul-timodal (reflecting the nature of the underlying error function, the term -L); and the determination of the normalization factor (also called the evidence;) is very difficult. Furthermore, the hyperparameters must be integrated out, since they are only used to determine the form of the distributions.
A solution is to integrate out the parameters separately from the hyperparameters, by making a Gaussian approximation; then, searching for the mode with respect to the hyperparameters (Bishop, 1995), (MacKay, 1992). This procedure gives a good estimation of the probability mass attached to the posterior, in particular for distributions over high-dimensional spaces, which is the case for large networks.
The Gaussian approximation is in practice derived by finding a maximum of the posterior distribution, and then evaluating the curvature of the distribution around the maximum:
The approximation thus is:
where the normalisation constant is simply evaluated from usual multivariate normal formulas.
The hyperparameters are calculated by finding the maximum of the approximate evidence ZMP. Alternate maximization (by using a nonlinear optimization algorithm) of the posterior and evidence is repeated until a self consistent solution (w.„, a,} is found. MP k
The full Bayesian treatment of inference implies that we do not simply get a pointwise prediction for functions f(x,t;w) of a model output, but a full distribution. Such predictive distributions have the form:
The above integrals are in general not analytically tractable, even when the posterior distribution over the parameters is Gaussian. However, it is usually enough to find the moments of the predictive distribution, in particular its mean and variance.A useful approximation is given by the delta method. Let f(w) be the function (of w) we wish to approximate. By Taylor expanding to first order around wMp, we can write:
Since this is a linear function of w, it will still be normally distributed under the Gaussian posterior, with mean and variance:
Error bars are simply obtained by taking the square root of the variance. We emphasize that it is important to evaluate first and second order information to understand the overall quality and reliability of a model's predictions. Error bars also provide hints on the distribution of the patterns (Williams et al., 1995) and can therefore be useful to understand whether a model is extrapolating its predictions. Furthermore, they can offer suggestions for the collection of future data (Williams et al., 1995; MacKay, 1992).
A Case Study: Ocular Melanoma
We show now an application ofthe CHENN model to the prognosis of all-cause mortality in ocular melanoma.
Intraocular melanoma occurs in a pigmented tissue called the uvea, with more than 90% of tumours involving the choroid, beneath the retina. About 50% of patients die of metastatic disease, which usually involves the liver.
Estimates for survival after treatment of uveal melanoma are mostly derived and reported using Cox analysis and Kaplan-Meier (KM) survival curves (Cox & Oakes). As a semiparametric model, the Cox method, however, usually utilizes linear relationships between variables, and the proportionality of risks is always assumed. It is therefore worth exploring the capability of nonlinear models, which do not make any assumptions about the proportionality of risks.
The data used to test the model were selected from the database of the Liverpool Ocular Oncology Centre (Taktak et al., 2004). The dataset was split into two parts, one for training (1823 patterns), the other one for test (781 patterns). Nine prognostic factors were used: Sex, Tumour margin, Largest Ultrasound Basal Diameter, Extraocular extension, Presence of epithelioid cells, Presence of closed loops, Mitotic rate, Monosomy of chromosome 3.
The performance of survival analysis models can in general be assessed according to their discrimination and calibration aspects. Discrimination is the ability of the model to separate correctly the subjects into different groups. Calibration is the degree of correspondence between the estimated probability produced by the model and the actual observed probability (Dreiseitl & Ohno-Machado, 2002). One of the most widely used methods for assessing discrimination in survival analysis is Harrell's C index (Dreiseitl & Ohno-Machado, 2002), (Harrell et al. 1982), an extension to survival analysis of the Area Under the Receiver Operator Characteristic (AUROC). Calibration is assessed by a Kolmogorov-Smirnov (KS) goodness-of-fit test with corrections for censoring (Koziol, 1980).
The C index was evaluated for a set of years that are of interest to applications, from 1 to 7. The minimum was achieved at 7 years (0.75), the maximum at 1 year (0.8). The KS test with corrections for censoring was applied for the above set of years, and up to the maximum uncensored time (16.8 years); the confidence level was set as usual at 0.05. The null hypothesis that the modeled distributions follow the empirical estimate cannot be rejected for years 1 to 7, whereas it is rejected if we compare the distributions up to 16.8 years; the null hypothesis is always rejected for the Cox model.
FUTURE TRENDS
Neural networks are very flexible modelling tools, and in the context of survival analysis they can offer advantages with respect to the (usually linear) modelling approaches commonly found in literature. This flexibility, however, comes at a cost: computational time and difficulty of interpretation of the model. The first aspect is due to the typically large number of parameters which characterise moderately complex networks, and the fact that the learning process results in a nonconvex, nonlinear optimization problem.
The second aspect is in some way a result of the nonlinearity and nonconvexity of the model. Addressing the issue of nonconvexity may be the first step to obtain models which can be easily interpreted in terms of their parameters, and easier to train; and in this respect, kernel machines (like Support Vector Machines) might be considered as the next step in flexible nonlinear modelling, although the formulation of learning algorithms for these models follows a paradigm which is not based on likelihood functions, and therefore their application to survival data is not immediate.
CONCLUSION
This article proposes a new neural network model for survival analysis in a continuous time setting, which approximates the logarithm of the hazard rate function. The model formulation allows an easy derivation of error bars on both hazard rate and survival predictions. The model is trained in the Bayesian framework to increase its robustness and to reduce the risk of overfitting. The model has been tested on real data, to predict survival from intraocular melanoma.
Formal discrimination and calibration tests have been performed, and the model shows good performance within a time horizon of 7 years, which is found useful for the application at hand.
KEY TERMS
Bayesian Inference: Inference rules which are based on application of Bayes' theorem and the basic laws of probability calculus.
Censoring: Mechanism which precludes observation of an event. A form of missing data.
Hyperparameter: Parameter in a hierarchical problem formulation. In Bayesian inference, the parameters of a prior.
Neural Networks: A graphical representation of a nonlinear function. Usually represented as a directed acyclic graph. Neural networks can be trained to find nonlinear relationships in data, and are used in applications such as robotics, speech recognition, signal processing or medical diagnosis.
Posterior Distribution: Probabilistic representation of knowledge, resulting from combination of prior knowledge and observation of data.
Prior Distribution: Probabilistic representation of prior knowledge.
Random Variable: Measurable function from a sample space to the measurable space of possible values of the variable.
Survival Analysis: Statistical analysis of data represented in terms of realisation of point events. In medical applications usually the point event is the death of an individual, or recurrence of a disease.