INTRODUCTION
Constraints appear in many areas of human endeavour starting from puzzles like crosswords (the words can only overlap at the same letter) and recently popular Sudoku (no number appears twice in a row) through everyday problems such as planning a meeting (the meeting room must accommodate all participants) till solving hard optimization problems for example in manufacturing scheduling (a job must finish before another job). Though all these problems look like being from completely different worlds, they all share a similar base - the task is to find values of decision variables, such as the start time of the job or the position of the number at a board, respecting given constraints. This problem is called a Constraint Satisfaction Problem (CSP).
Constraint processing emerged from AI research in 1970s (Montanary, 1974) when problems such as scene labelling were studied (Waltz, 1975). The goal of scene labelling was to recognize a type of line (and then a type of object) in the 2D picture of a 3D scene. The possible types were convex, concave, and occluding lines and the combination of types was restricted at junctions of lines to be physically feasible. This scene labelling problem is probably the first problem formalised as a CSP and some techniques developed for solving this problem, namely arc consistency, are still in the core of constraint processing. Systematic use of constraints in programming systems has started in 1980s when researchers identified a similarity between unification in logic programming and constraint satisfaction (Gallaire, 1985) (Jaffar & Lassez, 1987). Constraint Logic Programming was born. Today Constraint Programming is a separate subject independent of the underlying programming language, though constraint logic programming still plays a prominent role thanks to natural integration of constraints into a logic programming framework.
This article presents mainstream techniques for solving constraint satisfaction problems. These tech niques stay behind the existing constraint solvers and their understanding is important to exploit fully the available technology.
BACKGROUND
Constraint Satisfaction Problem is formally defined as a triple: a finite set of decision variables, a domain of possible values, and a finite set of constraints restricting possible combinations of values to be assigned to variables. Although the domain can be infinite, for example real numbers, frequently, a finite domain is assumed. Without lost of generality, the finite domain can be mapped to a set of integers which is the usual case in constraint solvers. This article covers finite domains only. In many problems, each variable has its own domain which is a subset of the domain from the problem definition. Such domain can be formally defined by a unary constraint. We already mentioned that constraints restrict possible combinations of values that the decision variables can take. Typically, the constraint is defined over a subset of variables, its scope, and it is specified either extensionally, as a set of value tuples satisfying the constraint, or intentionally, using a logical or arithmetical formula. This formula, for example A < B, then describes which value tuples satisfy the constraint. A small example of a CSP is ({A, B, C}, {1, 2, 3}, {A < B, B < C}).
The task of constraint processing is to instantiate each decision variable by a value from the domain in such a way that all constraints are satisfied. This instantiation is called a feasible assignment. Clearly, the problem whether there exists a feasible assignment for a CSP is NP-complete - problems like 3SAT or knapsack problem (Garey & Johnson, 1979) can be directly encoded as CSPs. Sometimes, the core constraint satisfaction problem is accompanied by a so called obj ective function defined over (some) decision variables and we get a Constrained Optimisation Problem. Then the task is to select among the feasible assignments the assignment that minimizes (or maximizes) the value of the objective function. This article focuses on techniques for finding a feasible assignment but these techniques can be naturally extended to optimization problems via a well-known branch-and-bound technique (Van Hentenryck, 1989).
There are several comprehensive sources of information about constraint satisfaction starting from journal surveys (Kumar, 1992) (Jaffar & Maher, 1996) through on-line tutorials (Bartak, 1998) till several topics. Van Hentenryck's topic (1989) was a pioneering work showing constraint satisfaction in the context of logic programming. Later Tsang's topic (1993) focuses on constraint satisfaction techniques independently of the programming framework and it provides full technical details of most algorithms described later in this article. Recent topics cover both theoretical (Apt, 2003) and practical aspects (Marriott & Stuckey, 1998), provide good teaching material (Dechter, 2003) or in-depth surveys of individual topics (Rossi et al., 2006). We should not forget about topics showing how constraint satisfaction technology is applied in particular areas; scheduling problems play a prominent role here (Baptiste et al., 2001) because constraint processing is exceptionally successful in this area.
CONSTRAINT SATISFACTION TECHNIQUES
Constraint satisfaction problems over finite domains are basically combinatorial problems so they can be solved by exploring the space of possible (partial or complete) instantiations of decision variables. Later in this section we will present the typical search algorithms used in constraint processing. However, it should be highlighted that constraint processing is not simple enumeration and we will also show how so called consistency techniques contribute to solving CSPs.
Systematic Search
Search is a core technology of artificial intelligence and many search algorithms have been developed to solve various problems. In case of constraint processing we are searching for a feasible assignment of values to variables where the feasibility is defined by the constraints. This can be done in a backtracking manner where we assign a value to a selected variable and check whether the constraints whose scope is already instantiated are satisfied. In the positive case, we proceed to the next variable. In the negative case, we try another value for the current variable or if there are no more values we backtrack to the last instantiated variable and try alternative values there. The following code shows the skeleton of this procedure called historically labelling (Waltz, 1975). Notice that the consistency check may prune domains of individual variables, which will be discussed in the next section.
The above backtracking mechanism is parameterized by variable and value selection heuristics that decide about the order of variables for instantiation and about the order in which the values are tried. While value ordering is usually problem dependent and problem-independent heuristics are not frequently used due to their computational complexity, there are popular problem-independent variable ordering heuristics. Variable ordering is based on a so called first-fail principle formulated by Haralick and Eliot (1980) which says that the variable whose instantiation will lead to a failure with the highest probability should be tried first. A typical instance of this principle is a dom heuristic which prefers variables with the smallest domain for instantiation. There exist other popular variable ordering heuristics (Rossi et al., 2006) such as dom+deg or domldeg, but their detail description is out scope of this short article.
Though the heuristics influence (positively) efficiency of search they cannot resolve all drawbacks of backtracking. Probably the main drawback is ignoring the information about the reason of constraint infeasi-bility. If the algorithm discovers that no value can be assigned to a variable, it blindly backtracks to the last instantiated variable though the reason of the conflict may be elsewhere. There exist techniques like back-jumping that can detect the variable whose instantiation caused the problem and backtrack (backjump) to this variable (Dechter, 2003). These techniques belong to a broader class of intelligent backtracking that shares the idea of intelligent recovery from the infeasibility. Though these techniques are interesting and far beyond simple enumeration, it seems better to prevent infeasibility rather than to recover from it (even in an intelligent way).
Domain Filtering and Maintaining Consistency
Assume variables A and B with domain {1, 2, 3} and a simple constraint A < B. Clearly, value 3 can never be assigned to A because there is no way to satisfy the constraint A < B if this value is used for A. Hence, this value can be safely removed from the domain of variable A and it does not need to be assumed during search. Similarly, value 1 can be removed from the domain of B. This process is called domain filtering and it is realised by a special procedure assigned to each constraint. Domain filtering is closely related to consistency of the constraint. We say that constraint C is (arc) consistent if for any value x in the domain of any variable in the scope of C there exist values in the domains of other variables in the scope of C such that the value tuple satisfies C. Such value tuple is called a support for x. Domain filtering attempts to make the constraint consistent by removing values which have no support.
Domain filtering can be applied to all constraints in the problem to remove unsupported values from the domains of variables and to make the whole problem consistent. Because the constraints are interconnected, it may be necessary to repeat the domain filtering of a constraint C if another constraint pruned the domain of variable in the scope ofC. Basically the domain filtering is repeated until a fixed point is reached which removes the largest number of unsupported values. There exist several procedures to realise this idea (Mackworth, 1977), AC-3 schema is the most popular one:
We did not cover the details ofthe filtering procedure here. In the simplest way, it may explore the consistent tuples in the constraint to find a support for each value. There exist more advanced techniques that keep some information between the repeated calls to the filter and hence achieve better time efficiency (Bessiere, 1994). Frequently, the filtering procedure exploits semantics of the constraint to realise filtering faster. For example, filtering for constraint A < B can be realised by removing from the domain of A all values greater than the maximal value of B (and similarly for B).
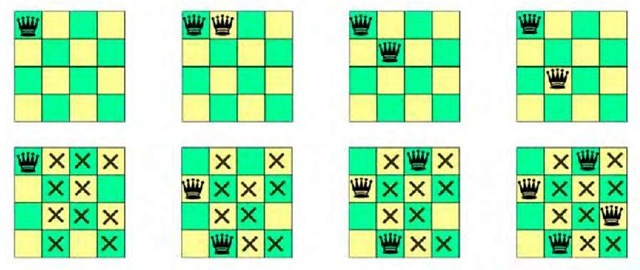
Let us return our attention back to search. Even if we make all the constraints consistent, it does not mean that we obtained a solution. For example, the problem ({A, B, C}, {1, 2, 3}, {A * B, B * C}) is consistent in the above-described sense, but it has no solution. Hence consistency techniques need to be combined with backtracking search to obtain a complete constraint solver. First, we make the constraints consistent. Then we start the backtracking search as described in the previous section and after each variable instantiation, we make the constraints consistent again. It may happen that during the consistency procedure some domain becomes empty. This indicates inconsistency and we can backtrack immediately. Because the consistency procedure removes inconsistencies from the not yet instantiated variables, it prevents future conflicts during search. Hence this principle is called look ahead opposite to look back techniques that focus on recovery from discovered conflicts. The whole process is also called maintaining consistency during search and it can be realised by substituting the consistent procedure in labelling by the procedure AC-3. Figure 1 shows a difference between simple backtracking (top) and the look-ahead technique (bottom) when solving a well known 4-queens problem. The task is to allocate a queen to each column of the chessboard in such a way that no two queens attack each other. Notice that the look-ahead solved the method after four attempts while the simple backtracking is still allocating the first two queens.
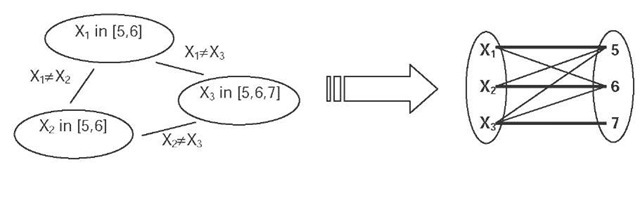
Clearly, the more inconsistencies one can remove, the smaller search tree needs to be explored. There exist stronger consistency techniques that assume several constraints together (rather that filtering each constraint separately, as we described above), but they are usually too computationally expensive and hence they are not used in each node of the search tree. Nevertheless, there also exists a compromise between stronger and efficient domain filtering called a global constraint. The idea is to encapsulate some well defined sub-problem into a single constraint (rather than a set of constraints) and then design a fast filtering algorithm for this constraint. A typical example of such global constraint is all-different that encapsulates a set of binary inequalities between all pairs of variables and by using filtering based on matching in bipartite graphs, it achieves stronger pruning (Regin, 1994). Figure 2 demonstrates how a CSP with binary inequalities is converted into a bipartite graph, where matching indicates a consistent instantiation of variables.
Figure 1. Solving 4-queens problem using backtracking (top) and look-ahead (bottom) techniques; the crosses indicate positions forbidden by the current allocation of queens in the look-ahead method (values pruned by AC).
Global constraints represent a powerful mechanism how to integrate efficient solving algorithms into general framework of constraint satisfaction. There exist dozens of global constraints designed for particular application areas (Baptiste et al., 2001) as well as general global constraints (Beldiceanu et al., 2005).
FUTURE TRENDS
Constraint processing is a mature technology that goes beyond artificial intelligence and co-operates (and competes) with techniques from areas such as operations research and discrete mathematics. Many constraint satisfaction techniques including dozens of specialized as well as generic global constraints have been developed in recent years (Beldiceanu et al., 2005) and new techniques are coming. The technology trend is to integrate the techniques from different areas for co-operative and hybrid problem solving. Constraint processing may serve as a good base for such integration (as global constraints showed) but it can also provide solving techniques to be integrated in other frameworks such as SAT (satisfaction of logical formulas in a conjunctive normal form). This " hybridization and integration" trend is reflected in new conferences, for example CP-AI-OR (International Conference on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems).
Figure 2. A graph representation of a constraint satisfaction problem with binary inequalities (left) and a bipartite graph representing the same problem in the all-different constraint (right).
The paradox of fast technology development is that the technology is harder to use by non-expert users. There always exists several ways how to model a problem using constraints and though the models are equivalent concerning their soundness, they are frequently not equivalent concerning their efficiency. Although there are several rules of "good constraint modelling" (Marriott & Stuckey, 1998) (Bartak, 2005) there do not exist generally applicable guidelines for constraint modelling. Hence it is sometimes not that easy to design a model that is solvable (in a reasonable time) by available constraint solvers. So one of the most important challenges of constraint processing for upcoming years is to bring the technology back to masses by providing automated modelling and problem reformulation tools that will form a middleware between the constraint solvers and non-expert users and make the holly grail of programming - the user states the problem and the computer solves it - a reality.
CONCLUSION
This article surveyed mainstream constraint satisfaction techniques with the goal to give a compact background of the technology to people who would like to use these techniques for solving combinatorial optimisation problems. We simplified the techniques and terminology a bit to fit the scope of the article while keeping the core principles. It is important to understand that the presented techniques (and even more) are already available in existing constraint solvers such us ILOG CP library (www.ilog.com/products/cp), SICStus Prolog (www.sics.se/sicstus), ECLiPSe (eclipse.crosscoreop. com), Mozart (www.mozart-oz.org), Choco (choco-solver.net) and other systems so the users are not required to program them from scratch. Nevertheless, understanding the underlying principles is important for design of efficient constraint models that can be solved by these systems. Constraint processing did not reach the holy grail of programming yet but it is going fast towards this goal.
KEY TERMS
Constrained Optimisation Problem (COP): A Constraint Satisfaction Problem extended by an objective function over the (subset of) decision variables. The task is to find a solution to the CSP which minimizes or maximizes the value of the objective function.
Constraint: Any relation between a subset of decision variables. Can be expressed extensionally, as a set of value tuples satisfying the constraint, or intentionally, using an arithmetical or logical formula between the variables, for example A+B < C.
Constraint Satisfaction Problem (CSP): A problem formulated using a set of decision variables, their domains, and constraints between the variables. The task is to find an instantiation of decision variables by values from their domains in such a way that all the constraints are satisfied.
Consistency Techniques: Techniques that remove inconsistent values (from variables' domains) or value tuples, that is, the values that cannot be assigned to a given variable in any solution. Arc consistency is the most widely used consistency technique.
Decision Variable: A variable modelling some feature of the problem, for example a start time of activity, whose value we are looking for in such a way that specified constraints are satisfied.
Domain of Variable: A set of possible values that can be assigned to a decision variable, for example a set of times when some activity can start. Constraint processing usually assumes finite domains only.
Domain Pruning (Filtering): A process of removing values from domains of variables that cannot take part in any solution. Usually, due to efficiency issues only the values locally violating some constraint are pruned. It is the most common type of consistency technique.
Global Constraint: An n-ary constraint modelling a subset of simpler constraints by providing a dedicated filtering algorithm that achieves stronger or faster domain pruning in comparison to making the simpler constraints (locally) consistent. All-different is an example of a global constraint.
LookAhead: The most common technique for integrating depth-first search with maintaining consistency. Each time a search decision is done, it is propagated in the problem model by making the model consistent.
Search Algorithms: Algorithms that explore the space of possible (partial or complete) instantiations of decision variables with the goal to find an instantiation satisfying all the constraints (and optimizing the objective function in case of COP).