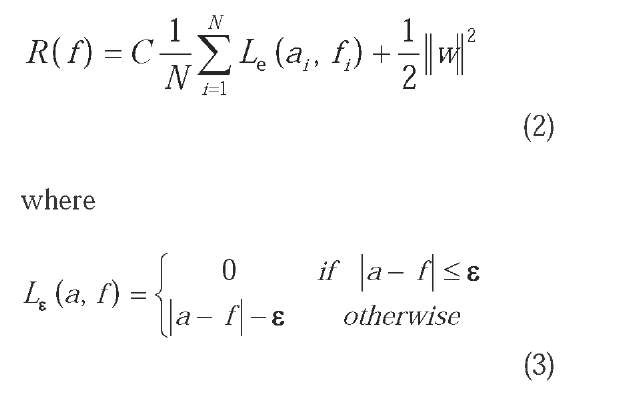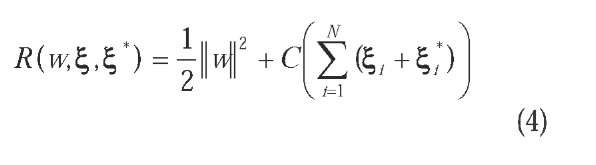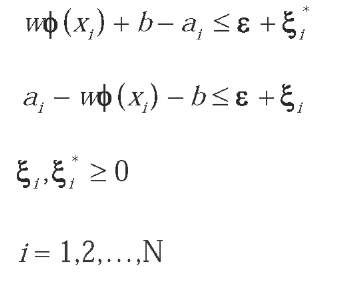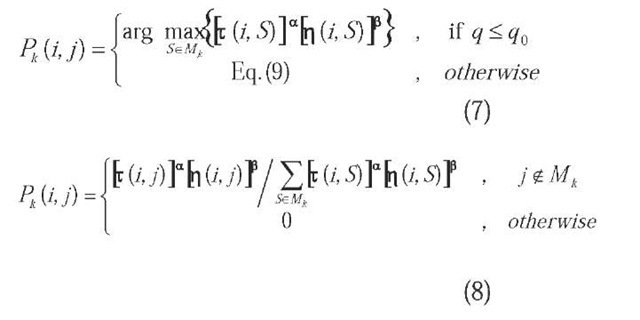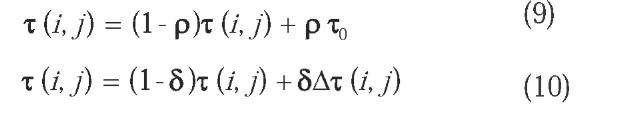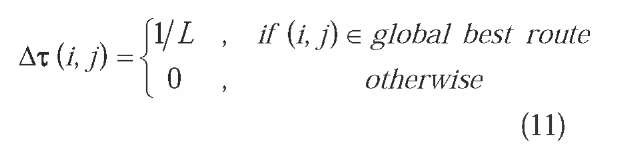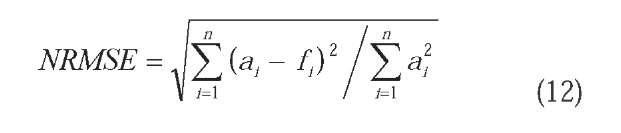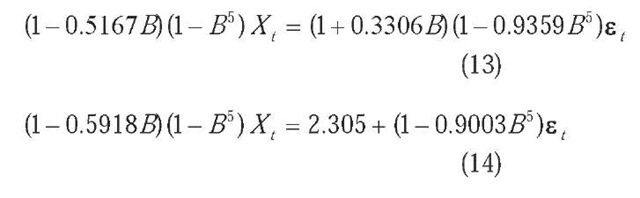Continuous ACO in a SVR Traffic Forecasting Model (Artificial Intelligence)

 

INTRODUCTION

The effective capacity of inter-urban motorway networks is an essential component of traffic control and information systems, particularly during periods of daily peak flow. However, slightly inaccurate capacity predictions can lead to congestion that has huge social costs in terms of travel time, fuel costs and environment pollution. Therefore, accurate forecasting of the traffic flow during peak periods could possibly avoid or at least reduce congestion. Additionally, accurate traffic forecasting can prevent the traffic congestion as well as reduce travel time, fuel costs and pollution.

However, the information ofinter-urban traffic presents a challenging situation; thus, the traffic flow forecasting involves a rather complex nonlinear data pattern and unforeseen physical factors associated with road traffic situations. Artificial neural networks (ANNs) are attracting attention to forecast traffic flow due to their general nonlinear mapping capabilities of forecasting. Unlike most conventional neural network models, which are based on the empirical risk minimization principle, support vector regression (SVR) applies the structural risk minimization principle to minimize an upper bound of the generalization error, rather than minimizing the training errors. SVR has been used to deal with nonlinear regression and time series problems. This investigation presents a short-term traffic forecasting model which combines SVR model with continuous ant colony optimization (SVRCACO), to forecast inter-urban traffic flow. A numerical example of traffic flow values from northern Taiwan is employed to elucidate the forecasting performance of the proposed model. The simulation results indicate that the proposed model yields more accurate forecasting results than the seasonal autoregressive integrated moving average (SARIMA) time-series model.

BACKGROUND

Traditionally, there has been a wide variety of forecasting approaches applied to forecast the traffic flow of inter-urban motorway networks. Those approaches could be classified according to the type of data, forecast horizon, and potential end-use (Dougherty, 1996); including historical profiling (Okutani & Stephanedes, 1984), state space models (Stathopoulos & Karlafits, 2003), Kalman filters (Whittaker, Garside & Lindveld, 1994), and system identification models (Vythoulkas, 1993). However, traffic flow data are in the form of spatial time series and are collected at specific locations at constant intervals of time. The above-mentioned studies and their empirical results have indicated that the problem of forecasting inter-urban motorway traffic flow is multi-dimensional, including relationships among measurements made at different times and geographical sites. In addition, these methods have difficultly coping with observation noise and missing values while modeling. Therefore, Danech-Pajouh and Aron (1991) employed a layered statistical approach with a mathematical clustering technique to group the traffic flow data and a separately tuned linear regre ssion model for each cluster. Based on the multi-dimensional pattern recognition requests, such as intervals of time and geographical sites, non-parametric regression models (Smith, Williams & Oswald, 2002) have also successfully been employed to forecast motorway traffic flow. The ARIMA model and extended models are the most popular approaches in traffic flow forecasting (Kamarianakis & Prastacos, 2005) (Smith et al., 2002). Due to the stochastic nature and the strongly nonlinear characteristics of inter-urban traffic flow data, the artificial neural networks (ANNs) models have received much attention and been considered as alternatives for traffic flow forecasting models (Ledoux, 1997) (Yin, Wong, Xu & Wong, 2002). However, the training procedure of ANNs models is not only time consuming but also possible to get trapped in local minima and subjectively in selecting the model architecture.

Thus, SVR have been successfully employed to solve forecasting problems in many fields. Such as financial time series (stocks index and exchange rate) forecasting (Pai & Lin, 2005) (Pai, Lin, Hong & Chen, 2006), engineering and software field (production values and reliability) forecasting (Hong & Pai, 2006) (Pai & Hong, 2006), atmospheric science forecasting (Hong & Pai, 2007) (Mohandes, Halawani, Rehman & Hussain, 2004), and so on. Meanwhile, SVR model had also been successfully applied to forecast electric load (Pai & Hong, 2005a) (Pai & Hong, 2005b). The practical results indicated that poor forecasting accuracy is suffered from the lack of knowledge of the selection of the three parameters (a, C, and s) in a SVR model.

In this investigation, one of evolutionary algorithms, the ant colony optimization (ACO), is tried to determine the values of three parameters in a SVR traffic flow model in Panchiao city of Taipei County, Taiwan. In addition, as being developed for discrete optimization, the application of ACO to continuous optimization problems requires the transformation of a continuous search space to a discrete one by discretization of the continuous decision variables, which procedure is so-called CACO.

MAIN FOCUS OF THE CHAPTER

In this article, two models, the seasonal ARIMA (SARIMA) model and the SVRCACO model, are used to compare the forecasting performance of traffic flow.

Support Vector Regression (SVR) Model

The basic concept of the SVR is to map nonlinearly the original data x into a higher dimensional feature space. Hence, given a set of data G = {(xt, at)} Nx (where x. is the input vector; a. is the actual value, and Nis the total number of data patterns), the SVM regression function is:

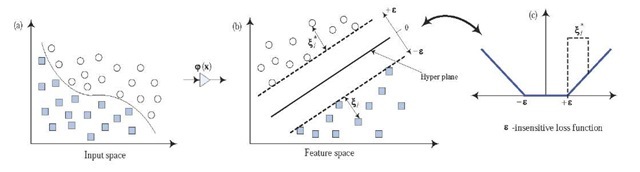
where f (x^ is the feature of inputs (to map the input data into a so-called high dimensional feature space, see Fig. 1 (a) and (b)), and both wand b are coefficients. The coefficients (w and b) are estimated by minimizing the following regularized risk function

In addition, Ls (a, f) is employed to find out an optimum hyper plane on the high dimensional feature space to maximize the distance separating the training data into two subsets. Thus, the SVR focuses on finding the optimum hyper plane and minimizing the training error between the training data and the s-insensitive loss function (as thick line in Fig. 1(c)).

Minimize:

with the constraints,

The first term of Eq. (5), employed the concept of maximizing the distance of two separated training data, is used to regularize weight sizes, to penalize large weights, and to maintain regression function flatness. The second term penalizes training errors of forecasting values and actual values by using the s-insensitive loss function. C is a parameter to trade off these two terms. Training errors above s are denoted as whereas training errors below s are denoted as %.

After the quadratic optimization problem with inequality constraints is solved, the weight w in Eq. (2) is obtained,

Figure 1. Transformation process illustration of a SVR model

Hence, the regression function is Eq. (6):

Here, K(x, x) is called the Kernel function. The value of the Kernel equals the inner product of two vectors, x. and x, in the feature space f (x^ and f (x); that is, K(x, x) = f (x) * f (x). The Gaussian RBF kernel is not only easier to implement, but also capable to nonlinearly map the training data into an infinite dimensional space, thus, it is suitable to deal with nonlinear relationship problems. In this work, the Gaussian function, exp(-||x- xj2 /2a2), is used in the SVR model. i

CACO in Selecting Parameters of the SVR Model

Ant colony optimization algorithms (Dorigo, 1992) have been successfully used to dealing with combinatorial optimization problems such as job-shop scheduling (Colorni, Dorigo, Maniezzo & Trubian, 1994), traveling salesman problem (Dorigo & Gambardella, 1997), space-planning (Bland, 1999), quadratic assignment problems (Maniezzo & Colorni, 1999), and data mining (Parpinelli, Lopes & Freitas, 2002). ACO imitates the behaviors of real ant colonies as they forage for food, wherein each ant lays down the pheromone on the path to the food sources or back to the nest. The paths with more pheromone are more likely to be selected by other ants. Over time, a colony of ants will select the shortest path to the food source and back to the nest. Therefore, a pheromone trail is the most important process for individual ant to smell and select its route.

The probability, Pk(ij), that an ant k moves from city i to city j is expressed as Eq. (7),

where t(i,j) is the pheromone level between city i and city j, n (ij) is the inverse of the distance between cities i and j. In this study, the forecasting error represents the distance between cities. The a and b are parameters determining the relative importance of pheromone level and M is a set of cities in the next column of the city matrix for ant k. q is a random uniform variable [0,1] and the value q0 is a parameter. The values of a, b and q0 are set to be 8, 5 and 0.2 respectively.

Once ants have completed their tours, the most pheromone deposited by ants on the visited paths is considered as the information regarding the best paths from the nest to the food sources. Therefore, the pheromone dynamic updating plays the main role in real ant colonies searching behaviors. The local and global updating rules of pheromone are expressed as Eq.(9) and Eq(10) respectively.

where p is the local evaporation rate of pheromone, 0 < p < 1; t0 is the initial amount of pheromone deposited on each of the paths. In this work, the values of p and t0 are set to be 0.01 and 1 correspondingly. In addition, the approach proposed by Dorigo and Gambardella (1994) was employed here for generating the initial amount of pheromone. Global trail updating is accomplished according Eq.(10). The 5 is the global pheromone decay parameter, 0 < 5 < 1, and set to be 0.2 for this study. The Ax (i, j), expressed as Eq.(11), is used to increase the pheromone on the path of the solution.

where L is the length of the shortest route.

A Numerical Example and Experimental Results

The traffic flow data sets were originated from three Civil Motorway detector sites. The Civil Motorway is the busiest inter-urban motorway networks in Panchiao city, the capital of Taipei County, Taiwan. The major site was located at the center of Panchiao City, where the flow intersects an urban local street system, and it provided one way traffic volume for each hour in weekdays. Therefore, one way flow data for peak traffic are employed in this investigation, which includes the morning peak period (MPP; from 6:00 to 10:00) and the evening peak period (EPP; from 16:00 to 20:00). The data collection is conducted from February 2005 to March 2005, the number of traffic flow data available for MPP and EPP are 45 and 90 hours, respectively. For convenience, the traffic flow data are converted to equivalent of passengers (EOP), and both of these two peak periods show the seasonality of traffic data. In addition, traffic flow data are divided into three parts: training data (MPP 25 hours; EPP 60 hours), validation data (MPP 10 hours; EPP 15 hours) and testing data (MPP 10 hours; EPP 15 hours). The accuracy of forecasting models is measured by the normalized root mean square error (NRMSE), as given by Eq.(12).

where n is the number of forecasting periods; ai is the actual traffic flow value at period i; and fi is the forecasting traffic flow value at period i.

The parameter selection of forecasting models is important for obtaining good forecasting performance. For the SARIMA model, the parameters are determined by taking the first-order regular difference and first seasonal difference to remove non-stationary and sea-sonality characteristics. Using statistical packages, with no residuals autocorrelated and approximately white noise residuals, the most suitable models for these two morning/evening peak periods for the traffic data are

SARIMA(1,0,1) x (0,1,1) 5 with non-constant item and SARIMA(1,0,1) x (1,1,1) 5 with constant item, respectively. The equations used for the SARIMA models are presented as Eqs. (13) and (14), respectively.

For the SVRCACO model, a rolling-based forecasting procedure was conducted and a one-hour-ahead forecasting policy adopted. Then, several types of data-rolling are considered to forecast traffic flow in the next hour. In this investigation, the CACO is employed to determine suitable combination of the three parameters in a SVR model. Parameters of the SVRCACO models with the minimum testing NRMSE values were selected as the most suitable model for this investigation. Table 1 indicates that SVRCACO models perform the best when 15 and 35 input data are used for morning/evening traffic forecast respectively. Table 2 compares the forecasting accuracy of the SARIMA and SVRCACO models in terms of NRMSE. It is illustrated that SVRCACO models have better forecasting results than the SARIMA models.

FUTURE TRENDS

In this investigation, the SVRCACO model provides a convenient and valid alternative for traffic flow forecasting. The SVRCACO model directly uses historical observations from traffic control systems and then determines suitable parameters by efficient optimization algorithms. In future research, other factors and meteorological control variables during peak periods, such as driving speed limitation, important social events, the percentage of heavy vehicles, bottleneck service level and waiting time during intersection traffic signals can be included in the traffic forecasting model. In addition, some other advanced optimization algorithms for parameters selection can be applied for the SVR model to satisfy the requirement of real-time traffic control systems.

Table 1. Forecasting results and associated parameters of the SVRCACO models

Morning peak period					Evening peak period
Nos. of input data		Parameters		NRMSE of testing	Nos. of input data		Parameters		NRMSE of testing
	<j	C	8			<j	C	8
5	0.7286	2149.2	0.8249	0.3965	25	0.7277	9658.9	0.4176	0.1112
10	0.7138	1199.0	0.1460	0.3464	30	0.9568	9337.7	0.7741	0.1037
15	0.7561	2036.5	0.9813	0.2632	35	0.8739	6190.2	0.7619	0.1033
20	0.6858	2141.6	0.4724	0.2754	40	0.1528	6300.5	0.8293	0.1147
					45	0.5093	3069.9	0.7697	0.1077
					50	0.1447	8835.7	0.8616	0.1247
					55	0.5798	6299.1	0.5796	0.1041

Table 2. Forecasting results (unit: EOP)

Morning peak period	Evening peak period
Peak k Actual SARIMA SVRCACO periods	Peak ak Actual SARIMA SVRCACO periods
031106 1,317.5 1,363.77 2,190.9 031107 2,522.0 2,440.11 2,027.4 031108 2,342.0 2,593.91 2,140.4 031109 2,072.0 2,422.09 2,313.7 031110 1,841.5 2,459.87 2,053.4 031206 995.5 1,578.34 1,980.6 031207 1,457.0 2,569.92 1,704.1 031208 1,899.0 2,690.35 1,548.3 031209 1,870.5 2,505.38 1,521.0 031210 2,151.5 2,537.98 1,881.1	031016 2,310.5 2,573.84 2,229.1 031017 2,618.0 2,821.57 2,319.9 031018 2,562.0 3,107.01 2,300.8 031019 2,451.5 3,103.66 2,571.6 031020 2,216.5 3,011.80 2,447.2 031116 2,175.5 2,611.58 2,432.4 031117 2,577.0 2,859.31 2,169.4 031118 2,879.5 3,144.75 2,450.4 031119 2,693.0 3,141.40 2,598.4 031120 2,640.0 3,049.54 2,671.9 031216 2,146.5 2,649.32 2,628.5 031217 2,544.5 2,897.05 2,633.1 031218 2,873.0 3,182.49 2,538.0 031219 2,567.5 3,179.13 2,670.8 031220 2,660.5 3,087.28 2,562.7
NRMSE 0.3039 0.2632	NRMSE 0.1821 0.1033

CONCLUSION

Accurate traffic forecast is crucial for the inter-urban traffic control system, particularly for avoiding congestion and for increasing efficiency of limited traffic resources during peak periods. The historical traffic data of Panchiao City in northern Taiwan shows a seasonal fluctuation trend which occurs in many inter-urban traffic systems. Therefore, over-prediction or under-pre-diction of traffic flow influences the transportation capability of an inter-urban system. This study introduces the application of forecasting techniques, SVRCACO, to investigate its feasibility for forecasting inter-urban motorway traffic. This article indicates that the SVR-CACO model has better forecasting performance than the SARIMA model. The superior performance of the SVRCACO model is due to the generalization ability of SVR model for forecasting and the proper selection of SVR parameters by CACO.

KEY TERMS

Ant Colony Optimization Algorithm (ACO): Inspired by the behavior of ants in finding paths from the colony to food, is a probabilistic technique for solving computational problems which can be reduced to 416 finding good paths through graphs. A short path gets marched over faster, and thus the pheromone density remains high as it is laid on the path as fast as it can evaporate.

Artificial Neural Networks (ANNs): A network of many simple processors ("units" or "neurons") that imitates a biological neural network. The units are connected by unidirectional communication channels, which carry numeric data.

Autoregressive Integrated Moving Average (ARIMA): A generalization of an autoregressive moving average (ARMA) model. These models are fitted to time series data either to better understand the data or to predict future points in the series. The model is generally referred to as an ARIMA(p, d,q) model where p, d, and q are integers greater than or equal to zero and refer to the order of the autoregressive, integrated, and moving average parts of the model respectively.

Evolutionary Algorithm (EA): is a generic population-based meta-heuristic optimization algorithm. An EA uses some mechanisms inspired by biological evolution: reproduction, mutation, recombination, natural selection and survival ofthe fittest. Evolutionary algorithms consistently perform well approximating solutions to all types of problems because they do not make any assumption about the underlying fitness landscape.

Pheromone: A pheromone is a chemical that triggers an innate behavioral response in another member of the same species. There are alarm pheromones, food trail pheromones, sex pheromones, and many others that affect behavior or physiology. In this article, food trail pheromones are employed, which are common in social insects.

Seasonal Autoregressive Integrated Moving Average (SARIMA): A kind of ARIMA model to conduct forecasting problem while seasonal effect is suspected. For example, consider a model of daily road traffic volumes. Weekends clearly exhibit different behavior from weekdays. In this case it is often considered better to use a SARIMA (seasonalARIMA) model than to increase the order of the AR or MA parts of the model.

Support Vector Machines (SVMs): Support vector machines (SVMs) were originally developed to solve pattern recognition and classification problems. With the introduction of Vapnik's s-insensitive loss function, SVMs have been extended to solve nonlinear regression estimation problems which are so-called support vector regression (SVR). SVR applies the structural risk minimization principle to minimize an upper bound of the generalization error. SVR has been used to deal with nonlinear regression and time series problems.