INTRODUCTION
Systems such as robotic systems and systems with large input-output data tend to be difficult to model using mathematical techniques. These systems have typically high dimensionality and have degrees of uncertainty in many parameters.Artificial intelligence techniques such as neural networks, fuzzy logic, genetic algorithms and evolutionary algorithms have created new opportunities to solve complex systems. Application of fuzzy logic [Bai, Y., Zhuang H. and Wang, D. (2006)] in particular, to model and solve industrial problems is now wide spread and has universal acceptance. Fuzzy modelling or fuzzy identification has numerous practical applications in control, prediction and inference. It has been found useful when the system is either difficult to predict and or difficult to model by conventional methods. Fuzzy set theory provides a means for representing uncertainties. The underlying power of fuzzy logic is its ability to represent imprecise values in an understandable form. The majority of fuzzy logic systems to date have been static and based upon knowledge derived from imprecise heuristic knowledge of experienced operators, and where applicable also upon physical laws that governs the dynamics of the process.
Although its application to industrial problems has often produced results superior to classical control, the design procedures are limited by the heuristic rules of the system. It is simply assumed that the rules for the system are readily available or can be obtained. This implicit assumption limits the application of fuzzy logic to the cases of the system with a few parameters. The number of parameters of a system could be large. The number of fuzzy rules of a system is directly dependent on these parameters. As the number of parameters increase, the number of fuzzy rules of the system grows exponentially.
Genetic Algorithms can be used as a tool for the generation of fuzzy rules for a fuzzy logic system. This automatic generation of fuzzy rules, via genetic algorithms, can be categorised into two learning techniques, supervised and unsupervised. In this paper unsupervised learning of fuzzy rules of hierarchical and multi-layer fuzzy logic control systems are considered. In unsuper-vised learning there is no external teacher or critic to oversee the learning process. In other words, there are no specific examples ofthe function to be learned by the system. Rather, provision is made for a task-independent measure of the quality or representation that the system is required to learn. That is the system learns statistical regularities of the input data and it develops the ability to learn the feature of the input data and thereby create new classes automatically [Mohammadian, M., Nainar, I. and Kingham, M. (1997)].
To perform unsupervised learning, a competitive learning strategy may be used. The individual strings of genetic algorithms compete with each other for the "opportunity" to respond to features contained in the input data. In its simplest form, the system operates in accordance with the strategy that 'the fittest wins and survives'. That is the individual chromosome in a population with greatest fitness 'wins' the competition and gets selected for the genetic algorithms operations (cross-over and mutation). The other individuals in the population then have to compete with fit individual to survive.
The diversity of the learning tasks shown in this paper indicates genetic algorithm's universality for concept learning in unsupervised manner. A hybrid integrated architecture incorporating fuzzy logic and genetic algorithm can generate fuzzy rules for problems requiring supervised or unsupervised learning. In this paper only unsupervised learning of fuzzy logic systems is considered. The learning of fuzzy rules and internal parameters in an unsupervised manner is performed using genetic algorithms. Simulations results have shown that the proposed system is capable of learning the control rules for hierarchical and multi-layer fuzzy logic systems. Application areas considered are, hierarchical control of a network of traffic light control and robotic systems.
A first step in the construction of a fuzzy logic system is to determine which variables are fundamentally important. Any number of these decision variables may appear, but the more that are used, the larger the rule set that must be found. It is known [Raju, S., Zhou J. and Kisner, R. A. (1990), Raju G. V. S. and Zhou, J. (1993), Kingham, M., Mohammadian, M, and Stonier, R. J. (1998)], that the total number of rules in a system is an exponential function of the number of system variables. In order to design a fuzzy system with the required accuracy, the number of rules increases exponentially with the number of input variables and its associated fuzzy sets for the fuzzy logic system.A way to avoid the explosion of fuzzy rule bases in fuzzy logic systems is to consider Hierarchical Fuzzy Logic Control (HFLC) [Raju G. V. S. and Zhou, J. (1993)] .A learning approach based on genetic algorithms [Goldberg, D. (1989)] is discussed in this paper for the determination of the rule bases of hierarchical fuzzy logic systems.
THE GENETIC FUZZY RULE GENERATOR ARCHITECTURE
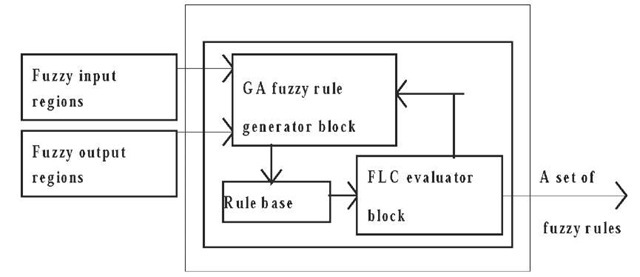
In this section we show how to learn the fuzzy rules in a fuzzy logic rule base using a genetic algorithm. The full set of fuzzy rules is encoded as a single string in the genetic algorithm population. To facilitate this we develop the genetic fuzzy rule generator whose architecture consists of five basic steps
1. Divide the input and output spaces of the system to be controlled into fuzzy sets (regions),
2. Encode the fuzzy rules into bit-string of 0 and 1,
3. Use a genetic algorithm as a learning procedure to generate set of fuzzy rules,
4. Use a fuzzy logic controller to assess the set of fuzzy rules and assign a value to each generated set of fuzzy rules,
5. Stop generating new sets of fuzzy rules once some performance criteria is met,
Figure 1 shows the genetic fuzzy rule generator architecture graphically. Suppose we wish to produce fuzzy rules for a fuzzy logic control with two inputs and single output. This simple two-input u1, u2 single-output y case is chosen in order to clarify the basic ideas of our new approach. Extensions to multi-output cases are straightforward. For more information on multi-output cases refer to Mohammadian et al [Mohammadian, M. and Stonier, R J., (1998)].
As a first step we divide the domain intervals of u1, u2 and y into different fuzzy sets. The number of the fuzzy sets is application dependent. Assume that we divide the interval for u1, u2 and y into 5, 7 and 7 fuzzy sets respectively. For each fuzzy set we assign a fuzzy membership function. Therefore a maximum of 35 fuzzy rules can be constructed for this system. Now the fuzzy rule base can be formed as a 5x7 table with cells to hold the corresponding actions that must be taken given the condition corresponding to u1, u2 are satisfied.
In step 2 we encode the input and output fuzzy sets into bit-strings (of 0 and 1). Each complete bit-string consists of 35 fuzzy rules for this example and each fuzzy rule base has the same input conditions but may have different output control signal assigned to it. Therefore we need only to encode the output signal of the fuzzy rule bit-strings into a complete bit-string. This will save the processing time for encoding and decoding of genetic algorithm's strings. In this case the length of an individual string has been reduced from 665 bits (i.e. 19x35) to 245 bits (i.e. 7x35). The choice of output control signal to be set for each fuzzy rule is made by the genetic algorithm. It initialises randomly a population of complete bit-strings. Each of these bit-strings is then decoded into fuzzy rules and evaluated by fuzzy logic controller to determine the fitness value for that bit-string. Application of proportional selection and mutation and one-point crossover operations can now proceed. Selection and crossover are the same as in simple genetic algorithms while the mutation operation is modified. Crossover and mutation take place based on the probability of crossover and mutation respectively. The mutation operator is changed to suit this problem, namely, an allele is selected at random and it is replaced by a random number ranging from 1 to 7 which represents in this example the five output fuzzy sets. The genetic algorithm process performs a self-directed search according to fitness value. In all applications in this paper we seek to minimise the fitness function. The process can be terminated after a desired number of generations or when the fitness value of the best string in a generation is less than some prescribed level.
Figure 1. Genetic fuzzy rule generator architecture
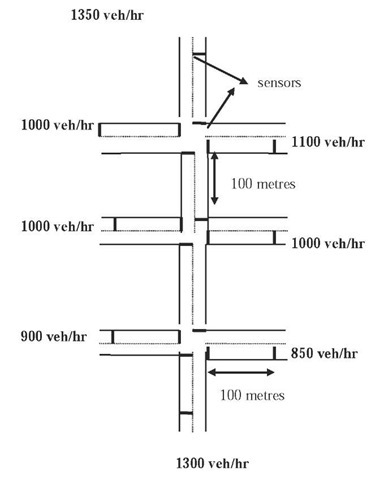
Figure 2. Three adjacent intersections
VARIABLE SELECTION AND RULE BASE DECOMPOSITION
Traffic Light Control
Traffic light control is widely used to resolve conflicts among vehicle movements at intersections. The control system at each signalised intersection consists of the following three control elements, cycle time, phase splits and offset. Cycle time is the duration of completing all phases of a signal; phase split is the division of the cycle time into periods of green phase for competing approaches; and offset is the time difference in the starting times of the green phases of adjacent intersections.
In [Nainar, I., Mohammadian, M., Stonier, R. J. and Millar, J. (1996)] a fuzzy logic control scheme is proposed to overcome the lack of interactions between the neighbouring intersections. First, a traffic model is developed and a fuzzy control scheme for regulating the traffic flow approaching a single traffic intersection is proposed. A new fuzzy control scheme employing a supervisory fuzzy logic controller is then proposed to coordinate the three intersections based on the traffic conditions at all three intersections. Simulation results established the effectiveness of proposed scheme. Figure 2 shows the three intersections used in the simulation.
A supervisory fuzzy logic control system is then developed to coordinate the three intersections far more effectively than the three local fuzzy logic control systems. This is because using supervisory fuzzy logic controller each intersection is coordinated with all its neighbouring intersections [Nainar, I., Mohammadian, M., Stonier, R. J. and Millar, J. (1996)]. The fuzzy knowledge base of the supervisory fuzzy logic controller was learnt using genetic algorithms. The supervisory fuzzy logic controller developed to coordinate the three intersections coordinated the traffic signals far more effectively than the three local fuzzy logic controllers. This is because using supervisory fuzzy logic controller each intersection is coordinated with all its neighbouring intersections. This proposed fuzzy logic control scheme can be effectively applied to on-line traffic control because of its ability to handle extensive traffic situations. Simulations results have shown that the multi-layer fuzzy logic system consisting of three local fuzzy logic controllers and the supervisory fuzzy logic controller is capable of reducing the waiting time on the network of the traffic intersections [Nainar, I., Mohammadian, M., Stonier, R. J. and Millar, J. (1996)].
Collision-Avoidance in a Robot System
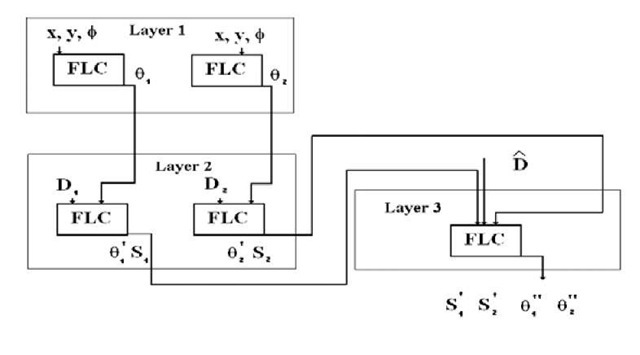
Consider the following collision-avoidance problem in a simulated, point mass, two robot system.A three-level hierarchical, fuzzy logic system was proposed to solve the problem, full details can be found in [Mohammadian, M. and Stonier, R. J. (1998)], see also [Mohammadian, M. and Stonier, R. J. (1995)]. In the first layer, two knowledge bases, one for each robot, are developed to find the steering angle to control each robot to its target. In the second layer two new knowledge bases are developed using the knowledge in the first layer to control the speed of each robot so that each robot approaches its target with near zero speed. Finally in the third layer, a single knowledge base is developed to modify the controls of each robot to avoid collision in a restricted common workspace, see Figure 3.
In Figure 3, x; y gives the physical position of the robot on the plane, <t is the directional heading of the robot, q is the steering angle, Dt and D2 are the distances of the two robots from there respective targets, S1 and S2 are the speeds of the two robots, D is the distance between the two robots and q1 , q2 , qj , q2 , s1 and s2 are the updates of variable outputs for the last two layers. An important issue in this example is that of learning knowledge in a given layer sufficient for use in higher layers. In the first layer of the hierarchical fuzzy logic system, ignoring the possibility of collision, steering angles for the control of each robot to their associated target were determined by genetic algorithms. In the second layer genetic algorithm was used to determine adjustments to steering angle and speed of each robot to control the speed of the robot when arriving to its target. Next another layer is developed to adjust the speed and steering angle of the robots to avoid collision of the robots. Consider the knowledge base of a single robot in layer one. It is not sufficient to learn a fuzzy knowledge base from an initial configuration and use this knowledge base for information on the steering angle of the robot to learn fuzzy controllers in the second layer. Quite clearly this knowledge base is only guaranteed to be effective from this initial configuration as not all the fuzzy rules will have fired in taking the robot to its target. We have to find a knowledge base that is effective to some acceptable measure, in controlling the robot to its target from 'any' initial configuration. One way is to first learn a set of local fuzzy controllers, each knowledge base learnt by an genetic algorithms from a given initial configuration within a set of initial configurations spread uniformly over the configuration space. These knowledge bases can then be fusedthrough a fuzzy amalgamation process [Stonier, R. J. and Mohammadian, M. (1995)] into the global (final), fuzzy control knowledge base. An alternative approach [Mohammadian, M. and Stonier, R. J. (1996), Stonier, R. J. and Mohammadian, M. (1998)], is to develop an genetic algorithms to learn directly the 'final' knowledge base by itself over the region of initial configurations.
Figure 3. Hierarchical structure for collision-avoidance
In conclusion the proposed hierarchical fuzzy logic system is capable of controlling the multi-robot system successfully. By using hierarchical fuzzy logic system the number of control laws is reduced. In the first layer of hierarchical fuzzy logic system ignoring the possibility of collision, steering angles for the control of each robot to their associated target were determined by genetic algorithms. In the second layer genetic algorithm was used to determine adjustments to steering angle and speed of each robot to control the speed of the robot when arriving to its target. Next another layer is developed to adjust the speed and steering angle of the robots to avoid collision of the robots. If only one fuzzy logic system was used to solve this problem with the inputs x, y, f of each robot and D each with the same fuzzy sets described in this paper then there would be 153125 fuzzy rule needed for its fuzzy knowledge base. Using a hierarchical fuzzy logic system there is a total number of 1645 fuzzy rules for this system. The hierarchical concept learning using the proposed method makes easier the development of fuzzy logic control systems, by encouraging the development of fuzzy logic controllers where the large number of systems parameters inhibits the construction of such controllers. For more details, we refer the reader to the cited papers.
ISSUES IN RULE BASE IDENTIFICATION
Research into this area has been described as genetic fuzzy systems using the classical genetic algorithm has been surveyed by Cordon [Cordon, O., Herrera, F. and Zwir, I. (2002)], see also [Cordon, O., Herrera, F., Hoffmann, F. and Magdalena, L. (2001)]. Genetic algorithms is employed to learn or tune different components of a fuzzy logic system such as the fuzzy knowledge base and the membership functions in the inference process. This is usually accomplished by using a genetic algorithms to produce the "best" fuzzy rules and membership functions/parameters with respect to an optimisation criterion. There are three main approaches in the literature for learning the rules in a fuzzy knowledge base. They are, the Pittsburgh approach, the Michigan approach and the iterative rule-learning approach [Cordon, O., Herrera, F., Hoffmann, F. and Magdalena, L. (2001)]. The Pittsburgh and Michigan approaches are the most commonly used methods in the area.
Research by the authors, colleagues and postgraduate students has predominately used the Pittsburgh approach with success in learning the fuzzy rules in complex systems, across hierarchical and multi-layered structures in problems [Stonier, R. J. and Zajaczkowski, J. (2003), Kingham, M., Mohammadian, M, and Stonier, R. J. (1998), Mohammadian, M. and Kingham, M. (2004), Mohammadian, M. (2002), Nainar, I., Mohammadian, M., Stonier, R. J. and Millar, J. (1996), Mohammadian, M. and Stonier, R. J. (1998), Stonier, R. J. and Mohammadian, M. (1995), Thomas, P. J. and Stonier, R. J. (2003), Thomas, P. J. and Stonier, R. J. (2003a)].
FUTURE TRENDS
In using the Pittsburgh approach the coding of the fuzzy rule base as a linear string in an evolutionary algorithm has its drawbacks other than the string may even be relatively large in length under decomposition into multi-layer and hierarchical structures. One is that this is a specific linear encoding of a nonlinear structure and typical one-point crossover when implemented introduces bias when reversing the coding to obtain the fuzzy logic rule base. Using co-evolutionary algorithms is also another option that needs further investigation.
CONCLUSION
This paper described the issues in the construction of a hierarchical fuzzy logic system to model a complex (nonlinear) system. The learning of fuzzy rules in such systems using genetic algorithms was proposed and it was shown to be feasible. Whilst the decomposition into hierarchical/multi-layered fuzzy logic sub-systems reduces greatly the number of fuzzy rules to be defined and to be learnt, other issues arise such as the decomposition is not unique and that it may give rise to variables with no physical significance. This can raise then major difficulties in obtaining a complete class of rules from experts even when the number of variables is small.
KEY TERMS
Fusing Variables: Fusing variables is a method for reducing the number of rules in a fuzzy rule base. The variables are fused (combined) together before input into the inference engine, thereby reducing the number of rules in the knowledge base.
Fuzzy Logic: Fuzzy sets and Fuzzy Logic were introduced in 1965 by Lotfi Zadeh as a new way to represent vagueness in applications. They are a generalisation of sets in conventional set theory. Fuzzy Logic (FL) aims at modelling imprecise models of reasoning, such as common sense reasoning for uncertain complex processes. A system for representing the meaning of lexically imprecise proposition in natural language structure through the proposition being represented as fuzzy constraints on a variable is provided. Fuzzy logic controllers have been applied to many nonlinear control systems successfully. Linguistic rather than crisp numerical rules are used to control the processes.
Fuzzy Rule Base (Fuzzy If-Then rules): Fuzzy If-Then or fuzzy conditional statements are expressions of the form "If A Then B", where A and B are labels of fuzzy sets characterised by appropriate membership functions. Due to their concise form, fuzzy If-Then rules are often employed to capture the imprecise modes of reasoning that play an essential role in the human ability to make decision in an environment of uncertainty and imprecision. The set of If-Then rules relate to a fuzzy logic system that are stored together is called a Fuzzy Rule Base.
GeneticAlgorithms: GeneticAlgorithms (GAs) are algorithms that use operations found in natural genetics to guide their way through a search space and are increasingly being used in the field of optimisation. The robust nature and simple mechanics of genetic algorithms make them inviting tools for search, learning and optimization. Genetic algorithms are based on computational models of fundamental evolutionary processes such as selection, recombination and mutation.
Genetic Algorithms Components: In its simplest form, a genetic algorithm has the following components:
1. Fitness - A positive measure of utility, called fitness, is determined for individuals in a population. This fitness value is a quantitative measure of how well a given individual compares to others in the population.
2. Selection - Population individuals are assigned a number of copies in a mating pool that is used to construct a new population. The higher a population individual's fitness, the more copies in the mating pool it receives.
3. Recombination - Individuals from the mating pool are recombined to form new individuals, called children. A common recombination method is one-point crossover.
4. Mutation - Each individual is mutated with some small probability << 1.0. Mutation is a mechanism for maintaining diversity in the population.
Hierarchical Fuzzy Logic Systems: The idea of hierarchical fuzzy logic control systems is to put the input variables into a collection of low-dimensional fuzzy logic control systems, instead of creating a single high dimensional rule base for a fuzzy logic control system. Each low-dimensional fuzzy logic control system constitutes a level in the hierarchical fuzzy logic control system. Hierarchical fuzzy logic control is one approach to avoid rule explosion problem. It has the property that the number of rules needed to construct the fuzzy system increases only linearly with the number of variables in the system
Unsupervised Learning: In unsupervised learning there is no external teacher or critic to oversee the learning process. In other words, there are no specific examples of the function to be learned by the system. Rather, provision is made for a task-independent measure of the quality or representation that the system is required to learn. That is the system learns statistical regularities of the input data and it develops the ability to learn the feature of the input data and thereby create new classes automatically.